
但未能从椭圆方程 +
+ = 1 ( a > 1 )中理会出| y | ≤ 1, 或未注意到a > 1的条件, 不对参数a分情况讨论, 就直接得出y =
= 1 ( a > 1 )中理会出| y | ≤ 1, 或未注意到a > 1的条件, 不对参数a分情况讨论, 就直接得出y =  时, | PQ | 取最大值
时, | PQ | 取最大值 , 导致失分;
, 导致失分;
 = (1
= (1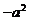 )
) 
 + 1 +
+ 1 +  ,
,
 = (1
= (1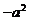 )
) -2y + 1 +
-2y + 1 + 
或
 =
=  +
+  ,
,
太繁, 而无法求解下去;
有的考生进行到求出
此题能够入手的多数考生都是循着解法1的路子做的. 有的考生写出 的表达式后, 意识不到条件“Q为椭圆上的一个动点”的作用, 不知道利用椭圆方程在
的表达式后, 意识不到条件“Q为椭圆上的一个动点”的作用, 不知道利用椭圆方程在 表达式中消元, 往下找不到深入的途径;
表达式中消元, 往下找不到深入的途径;
有的考生虽然想到了消元, 但消去的是y, 得到
注意到 | | ≤ 1, a > 1. 以下的讨论与解法1相同.
| ≤ 1, a > 1. 以下的讨论与解法1相同.
[错因分析] 本题求解中要用到椭圆的基本知识、两点间的距离、二次函数、求最值等知识, 解答过程蕴涵着函数思想、分类讨论等数学基本思想. 由于在这些方面以及思维的严谨性、周密性方面不同程度的欠缺, 造成了答题中不同层次的失误.
= (1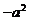 )
) -
- +
+ + 1.
+ 1.
= (1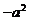 )
) -2
-2 +
+ + 1
+ 1
 =
= 
 +
+ 
设P (0, 1 ), Q ( ,
,  ), 则
), 则
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com