
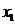 =
=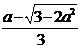 ,
, 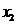 =
=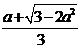 .
.
(iii) 若Δ= 12-8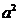 > 0, 即-
> 0, 即-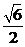 < a <
< a < 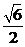 ,
, 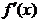 = 0 有二不同根
= 0 有二不同根
( ii) 若Δ= 12-8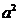 < 0, 抛物线在x轴上方, 恒有
< 0, 抛物线在x轴上方, 恒有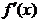 > 0,
> 0, 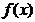 在(
在(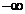 ,
, )为增函数. 所以
)为增函数. 所以 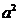 >
> 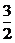 ,即a∈(
,即a∈(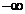 , -
, -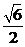 )∪(
)∪(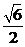 ,
,  ) .
) .
( i ) 若Δ= 12-8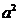 = 0 , 即a =±
= 0 , 即a =±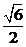 . 抛物线在x轴上方且与x轴相切与一点x =
. 抛物线在x轴上方且与x轴相切与一点x = 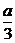 .当x∈(
.当x∈(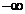 ,
,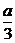 )或 x∈(
)或 x∈(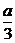 ,
, )时,
)时, 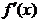 > 0,
> 0, 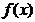 在(
在(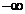 ,
, )为增函数. 所以a=±
)为增函数. 所以a=±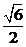 .
.
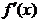 = 3
= 3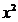 -2ax +
-2ax +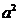 -1, 此函数图象为开口向上的抛物线, 其判别式 Δ= 4
-1, 此函数图象为开口向上的抛物线, 其判别式 Δ= 4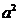 -12
-12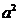 +12 = 12-8
+12 = 12-8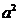 .
.
下面则转化为二次函数3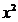 -2ax +
-2ax +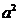 -1在区间 (
-1在区间 (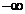 , 0 ) 和 ( 1,
, 0 ) 和 ( 1,  ) 上均为正的问题, 对于解决这个问题没有现成的定理可直接使用, 用纯代数的方法难以奏效, 必须借助图形来解决. 下面列出几种具体解法.
) 上均为正的问题, 对于解决这个问题没有现成的定理可直接使用, 用纯代数的方法难以奏效, 必须借助图形来解决. 下面列出几种具体解法.
解法1 利用抛物线与x轴的交点讨论.
求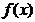 的导数, 得
的导数, 得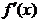 = 3
= 3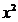 -2ax +
-2ax +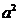 -1.
-1.
0.13
这是一道难题, 区分度很好. 本题得零分者有约37%之多. 得分集中在5分及其以下, 占56 %, 即最多求出了Δ≤0时a的取值范围. 能将Δ>0时a的取值情况讨论完整者很少, 总共不到2%. 得满分者占千分之五.
[考查意图] 本题主要考查导数的概念和计算、应用导数研究函数单调性的基本方法, 考查数形结合、分类讨论的数学思想和综合运用数学知识解决问题的能力.
[解答分析] 此题是一个利用导数来研究函数单调性的问题. 自然地, 首先求函数的导数, 把研究函数的增减性转化为研究导数的正、负.
1.87
设a为实数, 函数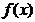 =
= 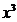 -a
-a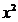 + (
+ (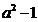 )x 在 (
)x 在 (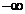 , 0 ) 和 ( 1,
, 0 ) 和 ( 1,  ) 都是增函数,求a的取值范围.
) 都是增函数,求a的取值范围.
[抽样统计数据]
题号
满分
平均分
难度
文(22)
14
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com