
综上, 得到 a ∈ ( , -
, - ]∪[1 ,
]∪[1 , 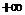 ).
).
类似地, 也可以利用抛物线顶点的纵坐标讨论. 如:
 , 解得
, 解得  . 所以 a ∈[1,
. 所以 a ∈[1, ).
).
(ii) 若Δ> 0, 为使 在 (
在 ( , 0 ) 和 ( 1,
, 0 ) 和 ( 1, 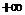 ) 为增函数, 只需
) 为增函数, 只需 ≥0,
≥0, ≥0且0 <
≥0且0 < < 1. 由
< 1. 由
即
a∈( , -
, - ]∪[1 ,
]∪[1 , 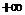 ).
).
解法2 利用抛物线的对称轴讨论.
(i) 若Δ≤0, 这种情况的求解与解法1相同, 不再赘述.
综上, a的取值范围为 ( , -
, - ]∪[
]∪[ ,
, 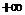 )∪[1 ,
)∪[1 ,  ).
).
由  ≤1 得
≤1 得 ≤3-a, 解得
-
≤3-a, 解得
- < a <
< a <  . 从而 a∈[1,
. 从而 a∈[1, ).
).
由  ≥0 得 a ≥
≥0 得 a ≥ , 解得1 ≤ a <
, 解得1 ≤ a <  .
.
为使 在(
在( , 0 )和( 1,
, 0 )和( 1, 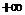 )为增函数, 必须
)为增函数, 必须 ≥0且
≥0且 ≤1.
≤1.
当x∈( ,
, )时,
)时,  < 0,
< 0,  为减函数.
为减函数.
当x∈( ,
, )或(
)或( ,
,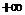 )时,
)时,  > 0,
> 0,  为增函数;
为增函数;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com