
还有的不明确Δ的取值, 就认定 ,
,  是
是 的二不同实根.
的二不同实根.
(5) 运算不熟练出现错误. 如, 解不等式组
③ 因为 在 (
在 ( , 0 ) 和 ( 1,
, 0 ) 和 ( 1, 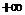 ) 为增函数, 所以
) 为增函数, 所以 在[0 , 1]上是减函数.
在[0 , 1]上是减函数.
② 因为 在 (
在 ( , 0 ) 和 ( 1,
, 0 ) 和 ( 1, 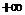 ) 为增函数, 所以
) 为增函数, 所以 >0,
>0,  >0.
>0.
① 因为 在 (
在 ( , 0 ) 和 ( 1,
, 0 ) 和 ( 1, 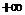 ) 为增函数, 所以
) 为增函数, 所以 >0.
>0.
(3) 对增减函数的性质、条件不够明确或对抛物线的性质特点不够清楚, 使得在分类讨论时, 分情况不恰当有遗漏或有重复. 如有的列出情况: Δ≥0 且 0 < < 1,
< 1,  >0,
>0,  >0; 也有的列出情况: Δ< 0 且
>0; 也有的列出情况: Δ< 0 且  >0,
>0,  >0. 前一种情况, 当Δ= 0时, 对于使
>0. 前一种情况, 当Δ= 0时, 对于使 >0, 条件0 <
>0, 条件0 < < 1,
< 1,  >0,
>0,  >0都是多余的; 当Δ> 0时, 0 <
>0都是多余的; 当Δ> 0时, 0 < < 1,
< 1,  >0,
>0,  >0是不完整的, 实际上, 其中的
>0是不完整的, 实际上, 其中的 >0,
>0,  >0 应为
>0 应为  ≥0,
≥0,  ≥0. 后一种情况, 因为有Δ< 0, 自然就有
≥0. 后一种情况, 因为有Δ< 0, 自然就有 >0,
>0,  >0, 所以是重复的.
>0, 所以是重复的.
(4) 部分考生推理不严谨或不正确. 举几例如下:
(2) 数形结合的数学思想不够明确, 求出 = 3
= 3 -2ax +
-2ax + -1 后, 不知结合
-1 后, 不知结合 的图象去讨论确定a的取值.
的图象去讨论确定a的取值.
(1) 对于求导数的方法未掌握或不熟练, 导致不会求 或出错.
或出错.
接下来, 通过 
 -1>0,
-1>0, 
 -1=0,
-1=0, 
 -1<0, 讨论曲线的位置, 确定参数a的取值.
-1<0, 讨论曲线的位置, 确定参数a的取值.
上述解答过程中虽未画出函数图象, 但推理是完全依赖于函数图象的.
[错因分析]
其图象为开口向上的抛物线, 知 =
= 
 -1为极小值, 也是最小值.
-1为极小值, 也是最小值.
 = 3
= 3 -2ax +
-2ax + -1 = 3
-1 = 3 +(
+(
 -1)
-1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com