2． ( 2007年湖南卷）已知则的最小值是   5    .

(A)4            (B)4           (C)2             (D)2

1．（ 2007年浙江卷）在平面直角坐标系中，不等式组表示的平面区域的面积是 (B )

（2007年北京卷）若三点共线，则的值等于____________.

㈡线性规划：以选择、填空题为主

（Ⅲ）求三棱锥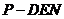的体积.

点评：本小题主要考查长方体的概念、直线和平面、平面和平面的关系等基础知识，以及空间想象能力和推理能力.

高考启示录---------解析几何

㈠直线基本知识的考查：选择填空题

（Ⅱ）求二面角的大小；

（Ⅰ）求证：面；

中点，分别是的中点，.

例4（2007四川卷）如图，在长方体中，分别是的

例3（2007江西卷）如图，在四面体ABCD中，截面AEF经过四面体的内切球（与四个面都相切的球）球心O，且与BC，DC分别截于E、F，如果截面将四面体分成体积相等的两部分，设四棱锥A－BEFD与三棱锥A－EFC的表面积分别是S₁，S₂，则必有（   ）

A.     S₁<S₂

B.     S₁>S₂

C.     S₁=S₂

D.     S₁，S₂的大小关系不能确定

分析：本题体现多面体和球体的综合，考查多面体的体积及面积等问题.

解析：连OA、OB、OC、OD，

则V_A－BEFD＝V_O－ABD＋V_O－ABE＋V_O－BEFD，

V_A－EFC＝V_O－ADC＋V_O－AEC＋V_O－EFC，又V_A－BEFD＝V_A－EFC，而每个三棱锥的高都是原四面体的内切球的半径，故S_ABD＋S_ABE＋S_BEFD＝S_ADC＋S_AEC＋S_EFC，又面AEF公共，故选C.

点评：割补的思想和方法是解决有关体积问题的重要手段.