
(Ⅱ)取bn= ,并用Sn表示
,并用Sn表示 PnFnGn的面积,试证:S1<S2且Sn<Sn+1 (n≥3).
PnFnGn的面积,试证:S1<S2且Sn<Sn+1 (n≥3).
点评:本题是解析几何、数列、不等式、函数的导数的综合问题,主要考查综合运用数学知识解决实际问题的能力.
高考启示录------概率统计
㈠排列组合
(Ⅰ)试证:bn≤ (n≥1);
(n≥1);
 2.( 2007年重庆卷)已知一列椭圆
2.( 2007年重庆卷)已知一列椭圆 .若椭圆Cn上有一点Pn使Pn到右准线ln的距离dn是|PnFn|与|PnGn|的等差中项,其中Fn、Gn分别是Cn的左、右焦点.
.若椭圆Cn上有一点Pn使Pn到右准线ln的距离dn是|PnFn|与|PnGn|的等差中项,其中Fn、Gn分别是Cn的左、右焦点.
(1)求证:“如果直线 过点T(3,0),那么
过点T(3,0),那么
 =
=
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
1.(2007年上海卷)在平面直角坐标系 O
O 中,直线
中,直线 与抛物线
与抛物线 =2
=2 相交于A、B两点.
相交于A、B两点.
(2)试问:当航天器在 轴上方时,观测点
轴上方时,观测点 测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
㈩综合问题
 (2007年上海春卷)学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为
(2007年上海春卷)学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为 ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以 轴为对称轴、
轴为对称轴、 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为 . 观测点
. 观测点 同时跟踪航天器.
同时跟踪航天器.
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(Ⅱ)设 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线 、
、 分别与椭圆相交于异于
分别与椭圆相交于异于 、
、 的点
的点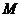 、
、 ,证明点
,证明点 在以
在以 为直径的圆内.
为直径的圆内.
(此题不要求在答题卡上画图)
点评:本小题主要考查直线、圆和椭圆等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力.
㈧定点和定值问题
(2007年全国卷II)已知抛物线x2=4y的焦点为F,A、B是抛物线上的两动点,且=λ(λ>0).过A、B两点分别作抛物线的切线,设其交点为M.
(Ⅰ)证明?为定值;
(Ⅱ)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.
点评:本题考查抛物线及其切线问题,同时渗透利用均值定理求最值问题,综合性较强,对考生解题能力要求较多.
㈨解析几何应用问题
 (Ⅰ)求椭圆的方程;
(Ⅰ)求椭圆的方程;
3.(2007年湖北卷)设 、
、 分别为椭圆
分别为椭圆 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且 为它的右准线.
为它的右准线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com