1．（2007年江西卷）某商场举行抽奖促销活动，抽奖规则是：从装有9个白球，1个红球的箱子中每次随机地摸出一个球，记下颜色后放回，摸出一个红球可获得奖金10元；摸出2个红球可获得奖金50元，现有甲，乙两位顾客，规定：甲摸一次，乙摸两次，令x表示甲，乙摸球后获得的奖金总额.求：

（1）x的分布列；   （2）x的的数学期望.

6．（2007年四川卷）某课程考核分理论与实验两部分进行，每部分考核成绩只记“合格”与“不合格”，两部分考核都是“合格”则该课程考核“合格”，甲、乙、丙三人在理论考核中合格的概率分别为；在实验考核中合格的概率分别为，所有考核是否合格相互之间没有影响，

（Ⅰ）求甲、乙、丙三人在理论考核中至少有两人合格的概率；

（Ⅱ）求这三人该课程考核都合格的概率.（结果保留三位小数）

点评：本小题主要考察相互独立事件、互斥事件、对立事件等概率的计算方法，考察应用概率知识解决实际问题的能力.满分12分.

㈤分布列、期望、方差

    假设某应聘者对三门指定课程考试及格的概率分别是，且三门课程考试是否及格相互之间没有影响.

    （Ⅰ）分别求该应聘者用方案一和方案二时考试通过的概率；

    （Ⅱ）试比较该应聘者在上述两种方案下考试通过的概率的大小.（说明理由）

点评：本题考查相互独立事件同时发生的概率以及利用作差比较法比较两个值大小的变形能力.

5．（2007年北京卷）某公司招聘员工，指定三门考试课程，有两种考试方案.

        方案一：考试三门课程，至少有两门及格为考试通过；

        方案二：在三门课程中，随机选取两门，这两门都及格为考试通过.

4．( 2007年湖南卷）某安全生产监督部门对5家小型煤矿进行安全检查(简称安检).若安检不合格,则必须进行整改.若整改后经复查仍不合格,则强行关闭.设每家煤矿安检是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5, 整改后安检合格的概率是0.8,计算(结果精确到0.01):

(Ⅰ)恰好有两家煤矿必须整改的概率;

(Ⅱ)平均有多少家煤矿必须整改;

(Ⅲ)至少关闭一家煤矿的概率.

点评：本题考查概率中的二项分布，P_n（k）公式等，考查学生分析问题解决问题的能力.

(Ⅱ)若取到的4个球中至少有2个红球的概率为，求n.

点评：本题主要考查排列组合、概率等基本知识，同时考查逻辑思维能力和数学应用能力.

3．（ 2007年浙江卷）甲、乙两袋装有大小相同的红球和白球，甲袋装有2个红球，2个白球；乙袋装有2个红球，n个白球.从甲，乙两袋中各任取2个球.

(Ⅰ)若n=3，求取到的4个球全是红球的概率；

     A．               B．     C．            D．

1．（2007年安徽卷）在正方体上任选3个顶点连成三角形，则所得的三角形是直角非等腰三角形的概率为（   ）

令，则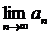=__1/2__.

㈣概率：

等可能事件（选择填空题）  对立事件、相互独立事件、独立重复事件（解答题综合）