
21.(本题满分12分)已知动点A、B分别在x轴、y轴上,且满足|AB|=2,点P在线段AB上,且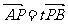 (t是不为零的常数).设点P的轨迹方程为C
(t是不为零的常数).设点P的轨迹方程为C
(1)求点P的轨迹方程C;
(2)若t=2,点M、N是C上关于原点对称的两个动点(M、N不在坐标轴上),点Q坐标为(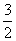 ,3),求ΔQMN的面积S的最大值
,3),求ΔQMN的面积S的最大值
20.(本小题满分12分)设函数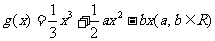 ,在其图象上一点P(x,y)
,在其图象上一点P(x,y)
处的切线的斜率记为f(x)
(1)若方程f(x)=0有两个实根分别为-2和4,求f(x)的表达式;
(2)若g(x)在区间[-1,3]上是单调递减函数,求a2+b2的最小值.
19.(本题满分12分)某国由于可耕地面积少,计划从今年起的五年填湖围造一部分生产和生活用地,若填湖费、购置排水设备费等所需经费与当年所填湖造地面积x(亩)的平方成正比,其比例系数为a,设每亩水面的年平均经济效益为b元,填湖造地后的每亩土地的年平均收益为c元(其中a,b,c均为常数,且c>b).
(1)若按计划填湖造地,且使得今年的收益不小于支出,试求所填面积x的最大值;
(2)如果填湖造地面积按每年l%的速度减少,为保证水面的蓄洪能力和环保要求,填湖造地的总面积不能超过现有水面面积的25%,求今年填湖造地的面积最多只能占现有水面的百分之几.
注:根据下列近似值进行计算:
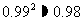 ,
, 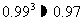 ,
,  ,
, 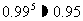 ,
, 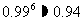 ,
, 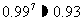
18.(本题满分12分)四棱锥P-ABCD中,PA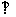 面ABCD,PA=AB=BC=2,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于只F, G, H,已知底面ABCD为直角梯形,AD∥BC,AB
面ABCD,PA=AB=BC=2,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于只F, G, H,已知底面ABCD为直角梯形,AD∥BC,AB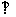 AD,∠BCD=135。.
AD,∠BCD=135。.
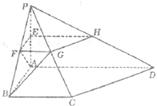
(1)求异面直线AF,BG所成的角的大小;
(2)设面APB与面CPD所成的锐二面角的大小为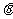 ,求cos
,求cos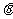 .
.
程或推演步骤.
17.(本题满分12分)
设函数f(x)=a•b,其中向量a=(2cosx ,1),b=(cosx, 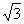 sin2x+m).
sin2x+m).
(1)求函数f(x)的最小正周期和在[0,π]上的单调递增区间;
(2)当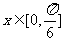 时,﹣4< f(x)<4恒成立,求实数m的取值范围.
时,﹣4< f(x)<4恒成立,求实数m的取值范围.
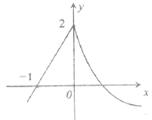
16.
函数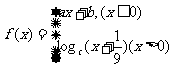 的图象如图所示,则a+b+c=
.
的图象如图所示,则a+b+c=
.
15.已知长方体ABCD-A1B1C1D1的外接球的半径为4,则ΔAA1B,ΔABD,ΔAA1D面积之和的最大值为 .
14.若数列{an}满足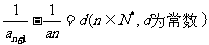 ,则称数列{ an
}为调和数列.已知数列{
,则称数列{ an
}为调和数列.已知数列{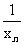 }为调和数列,且
}为调和数列,且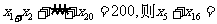 .
.
13.若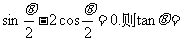 .
.
12.定义:若存在常数k,使得对定义域D内的任意两个不同的实数x1x2均有
|f(x1)-f(x2)|≤k|x1-x2|成立,则称函数f(x)在定义域D上满足利普希茨条件.对于函数,f(x)=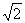 (x≥1)满足利普希茨条件,则常数k的最小值应是
(x≥1)满足利普希茨条件,则常数k的最小值应是
A.2 B.1 C.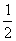 D.
D.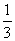
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com