
1.已知集合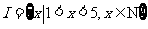 ,集合
,集合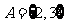 ,则
,则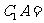 .
.
20.(本题满分22分,第1小题4分,第2小题6分,第3小题12分)
定义:将一个数列中部分项按原来的先后次序排列所成的一个新数列称为原数列的一个子数列.已知无穷等比数列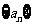 的首项、公比均为
的首项、公比均为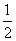 .
.
(1)试求无穷等比子数列 (
(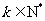 )各项的和;
)各项的和;
(2)是否存在数列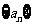 的一个无穷等比子数列,使得它各项的和为
的一个无穷等比子数列,使得它各项的和为 ?若存在,求出所有满足条件的子数列的通项公式;若不存在,请说明理由;
?若存在,求出所有满足条件的子数列的通项公式;若不存在,请说明理由;
(3)试设计一个数学问题,研究:是否存在数列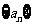 的两个(或两个以上)无穷等比子数列,使得其各项和之间满足某种关系.请写出你的问题以及问题的研究过程和研究结论.
的两个(或两个以上)无穷等比子数列,使得其各项和之间满足某种关系.请写出你的问题以及问题的研究过程和研究结论.
[第3小题说明:本小题将根据你所设计的问题的质量分层评分;问题的表达形式可以参考第2小题的表述方法.]
19.(本题满分16分,第1小题10分,第2小题6分)在某个旅游业为主的地区,每年各个月份从事旅游服务工作的人数会发生周期性的变化. 现假设该地区每年各个月份从事旅游服务工作的人数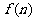 可近似地用函数
可近似地用函数 来刻画.其中:正整数
来刻画.其中:正整数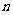 表示月份且
表示月份且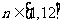 ,例如
,例如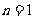 时表示1月份;
时表示1月份;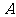 和
和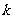 是正整数;
是正整数; .
.
统计发现,该地区每年各个月份从事旅游服务工作的人数有以下规律:
①各年相同的月份,该地区从事旅游服务工作的人数基本相同;
②该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差约400人;
③2月份该地区从事旅游服务工作的人数约为100人,随后逐月递增直到8月份达到最多.
(1)试根据已知信息,确定一个符合条件的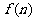 的表达式;
的表达式;
(2)一般地,当该地区从事旅游服务工作的人数超过400人时,该地区也进入了一年中的旅游“旺季”.那么,一年中的哪几个月是该地区的旅游“旺季”?请说明理由.
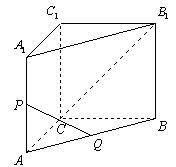
18.(本题满分15分,第1小题7分,第2小题8分)如图,在直三棱柱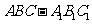 中,
中,
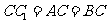 ,
,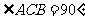 ,
,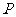 是
是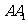 的中点,
的中点,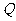 是
是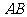 的中点.
的中点.
(1)求异面直线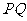 与
与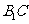 所成角的大小;
所成角的大小;
(2)若直三棱柱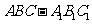 的体积为
的体积为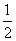 ,求四棱锥
,求四棱锥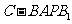 的体积.
的体积.
17.(本题满分14分,第1小题6分,第2小题8分)
已知关于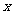 的不等式
的不等式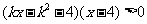 ,其中
,其中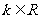 .
.
(1)当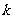 变化时,试求不等式的解集
变化时,试求不等式的解集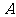 ;
;
(2)对于不等式的解集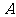 ,若满足
,若满足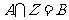 (其中
(其中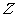 为整数集).试探究集合
为整数集).试探究集合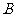 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合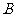 中元素个数最少的
中元素个数最少的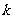 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合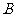 ;若不能,请说明理由.
;若不能,请说明理由.
16.(本题满分12分)设点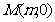 在椭圆
在椭圆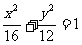 的长轴上,点
的长轴上,点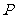 是椭圆上任意一点.当
是椭圆上任意一点.当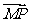 的模最小时,点
的模最小时,点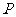 恰好落在椭圆的右顶点,求实数
恰好落在椭圆的右顶点,求实数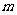 的取值范围.
的取值范围.
15.若不等式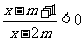 成立的一个充分非必要条件是
成立的一个充分非必要条件是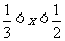 ,则实数
,则实数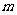 的取值范围是
( )
的取值范围是
( )
A.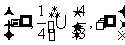 ; B.
; B. ; C.
; C. ; D.以上结论都不对.
; D.以上结论都不对.
14.设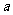 、
、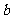 为两条直线,
为两条直线,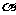 、
、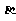 为两个平面.下列四个命题中,正确的命题是 ( )
为两个平面.下列四个命题中,正确的命题是 ( )
A.若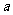 、
、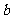 与
与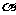 所成的角相等,则
所成的角相等,则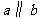 ;
;
B.若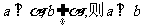 ;
;
C.若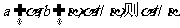 ;
;
D.若 ,
,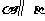 ,则
,则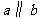 .
.
13.若平面向量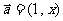 和
和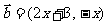 互相平行,其中
互相平行,其中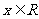 .则
.则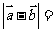 ( )
( )
A. 或0; B.
或0; B.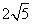 ; C.2或
; C.2或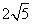 ; D.
; D. 或
或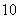 .
.
12.对任意的实数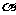 、
、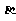 ,下列等式恒成立的是
(
)
,下列等式恒成立的是
(
)
A.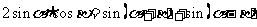 ;
;
B. ;
;
C.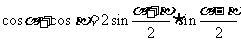 ;
;
D. .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com