

22.(本小题满分12 分)
已知函数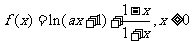 ,其中
,其中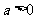
(Ⅰ)若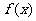 在x=1处取得极值,求a的值;
在x=1处取得极值,求a的值;
(Ⅱ)求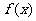 的单调区间;
的单调区间;
(Ⅲ)若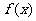 的最小值为1,求a的取值范围。
的最小值为1,求a的取值范围。
21.(本小题满分12 分)
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3 分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q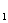 为0.25,在B处的命中率为q
为0.25,在B处的命中率为q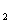 ,该同学选择先在A处投一球,以后都在B处投,用
,该同学选择先在A处投一球,以后都在B处投,用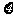 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
 |
0 |
2 |
3 |
4 |
5 |
|
p |
0.03 |
P1 |
P2 |
P3 |
P4 |
(Ⅰ)求q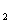 的值;
的值;
(Ⅱ)求随机变量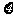 的数学期望E
的数学期望E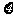 ;
;
(Ⅲ)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
20.(本小题满分12 分)
设函数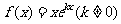
(Ⅰ)求曲线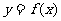 在点
在点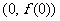 处的切线方程;
处的切线方程;
(Ⅱ)若函数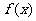 在区间
在区间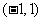 内单调递增,求
内单调递增,求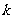 的取值范围。
的取值范围。
19.(本小题满分12 分)
某市决定新建“基础设施、民生和产业建设”三类工程,这三类工程所含项目的个数分别占总数的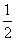 、
、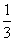 、
、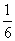 ,现在3名工人独立地从中任选一个项目参与建设。
,现在3名工人独立地从中任选一个项目参与建设。
(I)求他们选择的项目所属类别互不相同的概率;
(II)记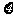 为3人中选择的项目属于基础设施工程或产业建设工程的人数,求
为3人中选择的项目属于基础设施工程或产业建设工程的人数,求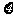 的分布列及数学期望。
的分布列及数学期望。
18.(本小题满分12 分)
是否存在常数a,b,c使得等式: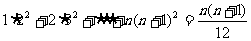
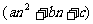 对一切正整数n都成立?证明你的结论。
对一切正整数n都成立?证明你的结论。
17.(本小题满分10分)
已知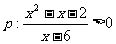 ,
, ,
,
若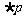 是
是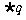 的充分而不必要条件,求实数
的充分而不必要条件,求实数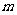 的取值范围。
的取值范围。
16.在半径为R的圆内,作内接等腰三角形,当底边上高为__________时它的面积最大。
15.已知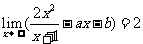 ,其中
,其中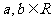 ,则
,则 的值为_________。
的值为_________。
14.不等式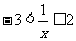 的解集是____________________。
的解集是____________________。
13.an是(1+x)n展开式中含x2的项的系数,则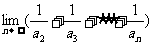 =___________。
=___________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com