
4.已知 为两条直线,
为两条直线, 为两个平面,给出下列命题,其中正确的是
为两个平面,给出下列命题,其中正确的是
A. B.
B.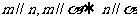
C. D.
D.
3.已知 ,则有
,则有
A. B.
B. C.
C. D.
D.
2.过点 且与直线
且与直线
 平行的直线方程为
平行的直线方程为
A.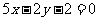 B.
B.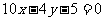
C. D.
D.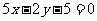
1.在等比数列 中,若
中,若 ,则
,则 等于
等于
A.4 B.8 C. D.
D.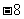
22.(本小题满分12分)
如图,平面内有一个定点F和一条定直线l的距离为2,动点P到l的距离d满足

(1)适当建立直角坐标系,求动点P的轨迹方程,并指出相应的点P的横、纵坐标的取值范围;
(2)在过F与l垂直的直线上有一点B,当点P运动时,若|PB|取最大值时点P不会在直线l上,求点B在(1)问所建立直角坐标系下的横坐标的取值范围。
21.(本小题满分12分)
如图为函数 轴和直线
轴和直线 分别交于点P、Q,点N(0,1),设△PQN的面积为
分别交于点P、Q,点N(0,1),设△PQN的面积为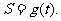

(1)求 的表达式;
的表达式;
(2)若 在区间
在区间 上单调递增,求n的最大值;
上单调递增,求n的最大值;
(3)若△PQN的面积为b时的点M恰好有两个,求b的取值范围。
20.(本小题满分12分)
某学校有三名教师到哈三中参观学习,被安排到某宾馆住宿,这个宾馆剩有三人间、四人间、五人间各一间,三人间每人每天住宿费160元,四人间每人每天住宿费130元,五人间每人每天住宿费100元。每位教师每天都等可能地被安排在三个房间的任一间,若这三位教师在此宾馆连续住5天。(每天都要重新安排)
求:(1)这三位教师第一天被安排在三个不同房间的概率;
(2)这三位教师住宿费之和至少有两天在320~370元的概率。(注:结果用最简分数作答)
19.(本小题满分12分)
已知数列
(1)求数列 的通项;
的通项;
(2)设
18.(本小题满分12分)
在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=AA1=1,D、E分别为棱AB、BC的中点,M为棱AA1上的点。

(1)证明:A1B1⊥C1D;
(2)当 的大小。
的大小。
17.(本小题满分10分)
设A、B、C为△ABC的三个内角,其对边分别a、b、c。
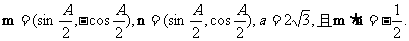
(1)求角A的大小;
(2)若 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com