
2.已知某市甲、乙、丙3个区共有高中生20000人,且甲、乙、丙3个区的高中生人数之比为2:3:5,现在要用分层抽样的方法从所有的学生中抽取一个容量为200的样本,乙区高中生应抽取 ( )
A.30 B.60 C.15 D.40
1.直线 、
、 、c两两平行,但不共面,则它们可以确实的平面个数是 ( )
、c两两平行,但不共面,则它们可以确实的平面个数是 ( )
A.1个 B.2个 C.3个 D.6个
22.(本题满分12分)
已知函数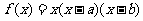 ,其中
,其中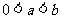 ,
, 在
在 及
及 处取得极值,其中
处取得极值,其中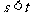 .
.
(1)求证: ;
;
(2)求证:点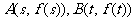 的中点
的中点 在曲线
在曲线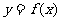 上;
上;
(3)若 ,求证:过原点且与曲线
,求证:过原点且与曲线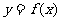 相切的两条直线不可能垂直.
相切的两条直线不可能垂直.
21.(本题满分12分)
已知数列 中,
中,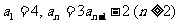 .
.
(1)求数列 的通项公式
的通项公式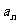 ;
;
(2)证明: .
.
20.(本题满分12分)
设抛物线 的焦点为F,准线为
的焦点为F,准线为 ,过点F作一直线与抛物线交于A、B两点,再分别过点A、B作抛物线的切线,这两条切线的交点记为P.
,过点F作一直线与抛物线交于A、B两点,再分别过点A、B作抛物线的切线,这两条切线的交点记为P.
(1)证明:直线PA与PB相互垂直,且点P在准线 上;
上;
(2)是否存在常数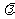 ,使等式
,使等式 恒成立?若存在,求出
恒成立?若存在,求出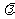 的值;若不存在,说明理由.
的值;若不存在,说明理由.
19.(本题满分12分)
已知数列 的前
的前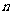 项和为
项和为 ,
,  ,且
,且 .
.
(1)计算 ;
;
(2)猜想 的表达式,并证明.
的表达式,并证明.
18.(本题满分12分)
在直四棱柱ABCD-A1B1C1D1中,已知底面四边形ABCD是边长为3的菱形,且DB=3,A1A=2,点E在线段BC上,点F在线段D1C1上,且BE=D1F=1.
(1)求证:直线EF∥平面B1D1DB;
(2)求二面角F-DB-C的余弦值.

17.(本题满分10分)
设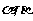 均为锐角,且
均为锐角,且 .求证:
.求证: .
.
16.将全体正奇数排成一个三角形数阵
1
3 5
7 9 11
13 15 17 19
21 23 25 27 29
… … … … … …
根据以上排列规律,数阵中第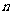 行的第一个数是________.
行的第一个数是________.
15.已知△ABC中,内角A,B,C所对的边分别是 ,AD⊥BC于D,则有
,AD⊥BC于D,则有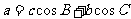 ,类比上述推理结论,写出下列条件下的结论:四面体P-ABC中,△ABC、△PAB、△PBC、△PCA的面积分别为S、S1、S2、S3,二面角P-AB-C、P-BC-A、P-AC-B的度数分别为
,类比上述推理结论,写出下列条件下的结论:四面体P-ABC中,△ABC、△PAB、△PBC、△PCA的面积分别为S、S1、S2、S3,二面角P-AB-C、P-BC-A、P-AC-B的度数分别为 ,则S=_____________________.
,则S=_____________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com