22．(本小题满分14分)

设椭圆C：+＝1(a>b>0)的一个顶点与抛物线C：x²＝4y的焦点重合，F₁、F₂分别是椭圆的左、右焦点，且离心率e＝．过椭圆右焦点F₂的直线l与椭圆C交于M、N两点．

(1)求椭圆C的方程；

(2)是否存在直线l，使得·＝－2？若存在，求出直线l的方程；若不存在，说明理由．

(3)若AB是椭圆C经过原点O的弦，MN∥AB，求证：为定值．

21．(本小题满分12分)

在数列{a_n}中，a₁＝2，a₂＝8，且已知函数f(x)＝(a_n+2－a_n+1)x³－(3a_n+1－4a_n)x(n∈N^*)在x＝1时取得极值．

(1)求数列{a_n}的通项a_n；

(2)设3ⁿb_n＝(－1)ⁿa_n，且|b₁|+|b₂|+…+|b_n|<m－3n()ⁿ⁺¹对于n∈N^*恒成立，求实数m的取值范围．

20．(本小题满分12分)

已知函数f(x)＝x³+(p－1)x²+qx(p，q为常数)．

(1)若f(x)在(x₁，x₂)上单调递减，在(－∞，x₁)和(x₂，+∞)上单调递增，且x₂－x₁>1，求证：p²>2(p+2q)；

(2)若f(x)在x＝1和x＝3处取得极值，且在x∈[－6,6]时，函数y＝f(x)的图象在直线l：15x－y+c＝0的下方，求c的取值范围．

19．(本小题满分12分)

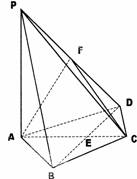
已知PA⊥平面ABCD，PA＝AB＝AD＝2，AC与BD交于E点，BD＝2，BC＝CD．

(1)取PD中点F，求证：PB∥平面AFC；

(2)求二面角A－PB－E的余弦角．

18．(本小题满分12分)

在2008年北京奥运会羽毛球女单决赛中，中国运动员张宁以2∶1力克排名世界第一的队友谢杏芳，蝉联奥运会女单冠军．羽毛球比赛按“三局二胜制”的规则进行(即先胜两局的选手获胜，比赛结束)，且各局之间互不影响．根据两人以往的交战成绩分析，谢杏芳在前两局的比赛中每局获胜的概率是0．6，但张宁在前二局战成1∶1的情况下，在第三局中凭借过硬的心理素质，获胜的概率为0．6．若张宁与谢杏芳下次在比赛上相遇．

(1)求张宁以2∶1获胜的概率；

(2)求张宁失利的概率．

17．(本小题满分12分)

已知函数g(x)＝－4cos²(x+)+4sin(x+)－a，把函数y＝g(x)的图象按向量a＝(－，1)平移后得到y＝f(x)的图象．

(1)求函数y＝log[f(x)+8+a]的值域；

(2)当x∈[－，]时，f(x)＝0恒有解，求实数a的取值范围．

16．已知命题

①函数f(x)＝在(0，+∞)上是减函数；

②函数f(x)的定义域为R，f′(x₀)＝0是x＝x₀为极值的既不充分也不必要条件；

③函数f(x)＝2sin xcos |x|的最小正周期为π；

④在平面内，到定点(2,1)的距离与到定直线3x+4y－10＝0的距离相等的点的轨迹是抛物线；

⑤已知a＝(3,4)，b＝(0，－1)，则a在b方向上的投影为4．

其中，正确的命题的序号是　　．(把你认为正确命题的序号都填上)

15．设(x²+2x－2)⁶＝a₀+a₁(x+2)+a₂(x+2)²+…+a₁₂(x+2)¹²，其中a_i(i＝0,1,2，…，12)为实常数，则a₁+a₂+…+a₁₂＝　　．

14．过点P(2,1)的直线与抛物线y²＝16x交于A、B两点，且+＝0，则此直线的方程为　　．

13．已知tan(α－)＝－，则＝　　．