4．(x－)⁹的展开式的第3项是

A．－84x³　 　　　　B．84x³ 　C．36x⁵　 　　　　D．－36x⁵

3．某大型超市销售的四种乳类商品：液态奶、酸奶、婴幼儿奶粉、成人奶粉分别有40种、10种、30种、20种不同的品牌，现从中抽取一个容量为20的样本进行三聚氰胺安全检测，若采用分层抽样的方法抽取样本，则抽取的酸奶与成人奶粉品牌数之和是

A．5 　　　　　　B．4 　　　　　C．7　　　　　 　D．6

2．已知{a_n}是等差数列，a₁＝15，S₅＝55，则过点P(3，a₂)，Q(4，a₄)的直线的斜率为

A．4 　　　　　　B． 　　　　　C．－4　 　　　　D．－

1．已知集合M＝{0,1,2}，N＝{x|x＝2a，a∈M}，则集合M∩N等于

A．{0}　　　B．{0,2}　　C．{1,2}　　D．{0,1}

22．(本小题12分)

　　 已知函数满足

　 (I)设上的最小值；

　 (II)证明：

　 (III)记

21．(本小题满分12分)

　　　 已知抛物线的顶点在坐标原点O，焦点F在x正半轴上，倾斜角为锐角的直线过F点。设直线与抛物线交于A、B两点，与抛物线的准线交于M点，

　 (I)若，求直线的斜率；

　 (II)若点A、B在x轴上的射影分别为A₁、B₁，且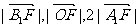成等差数列，求的值。

20．(本小题12分)

　　 某射手向一个气球射击，假定各次射击是相互独立的，且每次射击击破气球的概率均为。

　 (I)若该射手共射击三次，求第三次射击才将球击破的概率；

　 (II)给出两种积分方案：

　　　　 方案甲：提供三次射击机会和一张700点的积分卡，若未击中的次数为，则扣除积分128点。

　　　　　　　 方案乙：提供四次射击机会和一张1000点的积分卡，若未击中的次数为，则扣除积分256点。

　　　　　　　 在执行上述两种方案时规定：若将球击破，则射击停止；若未击破，则继续射击直至用完规定的射击次数。

　　　　　　　 问：该射手应选择哪种方案才能使积分卡剩余点数最多，并说明理由。

19．(本小题满分12分)

　 已知球O的半径为1，P、A、B、C四点都在球面上，面ABC，AB=AC，。

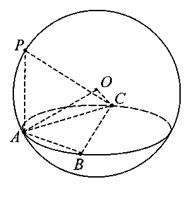
　 (I)证明：BA面PAC；

　 (II)若，求二面角O-AC-B的大小。

18．(本小题满分12分)

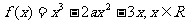
　 (I)当的单调区间；

　 (II)当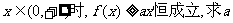的取值范围。

17．(本小题10分)

　　　 设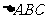的内角A、B、C所对的边长分别为a、b、c，且

　 (I)求的值；

　 (II)若的值。