
3.如果直线 的一条渐近线,那么该双曲线的离心率等于
的一条渐近线,那么该双曲线的离心率等于
( )
A. B.
B.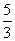 C.
C. D.2
D.2
2.数列 的前n项和为 ( )
的前n项和为 ( )
A. B.
B. C.
C. D.
D.
1.已知i是虚数单位,复数 在复平面内对应的点在 ( )
在复平面内对应的点在 ( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知:双曲线 方程为:
方程为: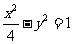 ,双曲线
,双曲线 方程为:
方程为: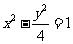
(1)分别求出它们的焦点坐标和渐近线方程;
(2)如图所示,过点 作斜率为3的直线分别与双曲线
作斜率为3的直线分别与双曲线 和双曲线
和双曲线 的右支相交。试判断线段
的右支相交。试判断线段 与
与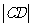 是否相等,并说明理由;
是否相等,并说明理由;
(3)过点 作直线
作直线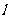 与双曲线
与双曲线 的右支和双曲线
的右支和双曲线 的右支相交,求直线
的右支相交,求直线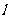 与双曲线
与双曲线 右支和双曲线
右支和双曲线 右支交点的总个数,并简要说明理由。
右支交点的总个数,并简要说明理由。

20.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知数列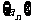 的首项
的首项 ,
, ,
, (
( )
)
(1)问数列 是否构成等比数列;
是否构成等比数列;
(2)若已知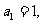 设无穷数列
设无穷数列 的各项和为
的各项和为 ,求
,求
(3)在(2)的条件下,设 (
(
 是常变量),若对任意
是常变量),若对任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
19.(本题满分14分) 本题共有2个小题,第1小题满分4分,第2小题满分10分.
若函数 同时满足以下条件:
同时满足以下条件:
①它在定义域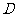 上是单调函数;
上是单调函数;
②存在区间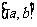

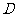 使得
使得 在
在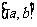 上的值域也是
上的值域也是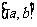 ,我们将这样的函数称作“
,我们将这样的函数称作“ 类函数”。
类函数”。
(1)函数 是不是“
是不是“ 类函数”?如果是,试找出
类函数”?如果是,试找出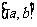 ;如果不是,试说明理由;
;如果不是,试说明理由;
(2)求使得函数 是“
是“ 类函数”的常数
类函数”的常数 的取值范围。
的取值范围。
18.(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图,在三棱锥 中,
中, ,
,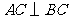 ,
,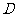 是
是 的中点,且
的中点,且 ,
, .
.

(I)求证:直线 平面
平面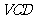 ;
;
(II)求直线 与平面
与平面 所成的角.
所成的角.
17.(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分.
如图所示为电流强度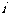 (安培)随时间
(安培)随时间 (秒)变化的关系式是:
(秒)变化的关系式是: (其中
(其中 >0)的图象。若点
>0)的图象。若点 是图象上一最低点。
是图象上一最低点。

(1)求 ,
, ;
;
(2)已知点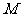 、点
、点 在图象上,点
在图象上,点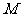 的坐标为
的坐标为 ,若点
,若点 的坐标为
的坐标为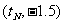 ,试用两种方法求出
,试用两种方法求出 的值。(精确到0.0001秒)
的值。(精确到0.0001秒)
16.设函数 在区间
在区间 上单调递增,现将
上单调递增,现将 的图象向右平移
的图象向右平移 个单位得到函数
个单位得到函数 ,则函数
,则函数 的单调递减区间必定是
的单调递减区间必定是
A. B.
B.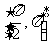
C. D.
D.
15.“ ”是“对任意的正数
”是“对任意的正数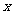 ,
, ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com