
20.(本小题满分13分)
已知数列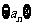 满足
满足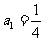 ,
,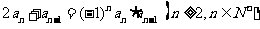 ,
,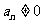 .
.
(Ⅰ)证明数列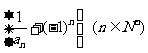 为等比数列,求出
为等比数列,求出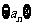 的通项公式;
的通项公式;
(Ⅱ)设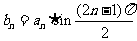 ,数列
,数列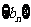 的前
的前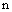 项和为
项和为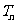 ,求证:对任意
,求证:对任意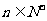 ,
,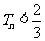 .
.
19.(本小题满分12分)
已知定义在R上的函数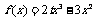 ,其中t为常数.
,其中t为常数.
(Ⅰ)当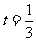 时,求函数
时,求函数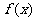 的极值;
的极值;
(Ⅱ)求函数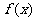 的单调递增区间.
的单调递增区间.
18.(本小题满分12分)
如图甲,直角梯形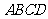 中,
中,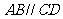 ,
,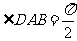 ,点
,点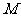 、
、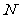 分别在
分别在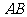 ,
,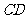 上,且
上,且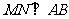 ,
,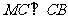 ,
,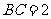 ,
,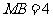 ,现将梯形
,现将梯形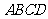 沿
沿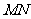 折起,使平面
折起,使平面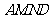 与平面
与平面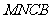 垂直(如图乙).
垂直(如图乙).
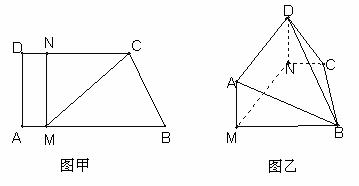
(Ⅰ)求证: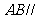 平面
平面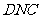 ;
;
(Ⅱ)当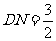 时,求二面角
时,求二面角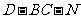 的大小.
的大小.
17.(本小题满分12分)
某校从参加计算机测试的学生中抽出60名学生,将其成绩(均为整数)分成六段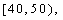
 后画出如下部分频率分布直方图. 观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图. 观察图形的信息,回答下列问题:
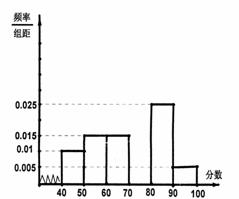
(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和利用各组中值估计这次考试平均分 (组中值即某组数据区间的中点值,如[60,80]的组中值为70) ;
(Ⅲ)从成绩是80分以上(包括80分)的学生中任选两人,求他们在同一分数段的概率.
16.(本小题满分12分)
在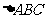 中,
中,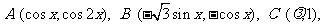 若
若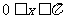 ,且
,且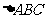 的重心在
的重心在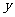 轴负半轴上,求实数
轴负半轴上,求实数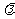 的取值范围.
的取值范围.
15.已知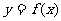 是R上偶函数,对于
是R上偶函数,对于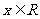 都有
都有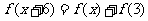 成立;且
成立;且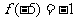 ;当
;当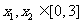 且
且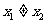 时,都有
时,都有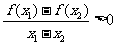 .则给出下列命题:①
.则给出下列命题:① 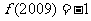 ;②直线
;②直线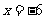 是函数
是函数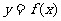 图像的一条对称轴;③
图像的一条对称轴;③ 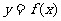 在
在 上为减函数;④方程
上为减函数;④方程 在
在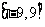 上有4个根。其中正确的命题为
上有4个根。其中正确的命题为
(填写正确命题的序号)
14.向量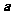 ,
,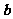 ,
,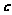 满足
满足 ,
,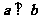 ,
,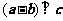 ,
,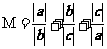 ,则M=________
,则M=________
12.已知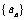 为等比数列,
为等比数列,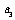 和
和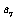 是方程
是方程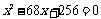 的两根,若
的两根,若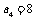 ,则
,则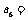 .
.
|
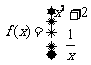
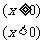 的反函数为
的反函数为 ,则
,则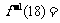
11.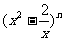 的展开式中,常数项为240,则
的展开式中,常数项为240,则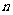 = .
= .
10.抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上.设抛物线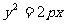
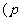 >
>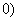 ,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为 ( )
,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为 ( )
A.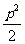 B.
B.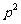 C.
C.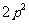 D.
D.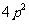
第Ⅱ卷(非选择,共100分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com