
20.(本小题满分12分)
已知公差不为0的等差数列 的前
的前 项和为
项和为 ,且满足
,且满足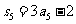 ,又
,又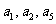 依次成等比数列,数列
依次成等比数列,数列 满足
满足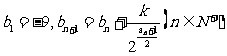 ,其中
,其中 为大于0的常数。
为大于0的常数。
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)记数列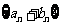 的前
的前 项和为
项和为 ,若当且仅当
,若当且仅当 时,
时, 取得最小值,求实数
取得最小值,求实数 的取值范围。
的取值范围。
19.(本小题满分12分)
如图ABCD是一个直角梯形,其中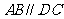 ,
, ,
,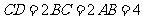 ,过点A作CD的垂线AE,垂足为点E,现将△ADE折起,使二面角
,过点A作CD的垂线AE,垂足为点E,现将△ADE折起,使二面角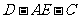 的大小是
的大小是 。
。

(1)求证:平面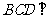 平面
平面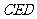 ;
;
(2)求点 到平面
到平面 的距离;
的距离;
(3)求二面角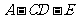 的大小。
的大小。
|
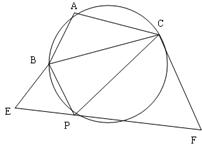
如图,圆内接三角形 的边长分别为
的边长分别为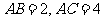 ,设
,设
(1)求弦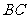 的长;
的长;
(2)设点P是 弧上的一动点(不与B,C重合且与A分别在BC的两侧),分别以PB,PC为一边作正三角形PBE、正三角形PCF,求这两个正三角形面积和的取值范围。
弧上的一动点(不与B,C重合且与A分别在BC的两侧),分别以PB,PC为一边作正三角形PBE、正三角形PCF,求这两个正三角形面积和的取值范围。
18.(本小题满分12分)
为应对金融危机,刺激消费,某市给市民发放面额为100元的旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
 |
200元 |
300元 |
400元 |
500元 |
|
老年 |
0.4 |
0.3 |
0.2 |
0.1 |
|
中年 |
0.3 |
0.4 |
0.2 |
0.1 |
|
青年 |
0.3 |
0.3 |
0.2 |
0.2 |
某天恰好有持有这种消费卷的老年人、中年人、青年人各一人到该旅游景点,
(1)求这三人恰有两人消费额大于300元的概率;
(2)求这三人消费总额大于或等于1300元的概率。
16.若数列 满足
满足 (
( 为常数),则称数列
为常数),则称数列 为调和数列。已知数列
为调和数列。已知数列 为调和数列,且
为调和数列,且 ,则
,则 = 。
= 。
15.某班一天上午有4节课,每节都需要安排一名教师去上课,现从A,B,C,D,E,F等6名教师中安排4人分别上一节课,第一节课只能从A、B两人中安排一人,第四节课只能从A、C两人中安排一人,则不同的安排方案共有 _________。
_________。
14.已知平面向量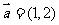 ,
,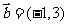 ,
, ,则
,则 与
与 夹角的余弦值为 。
夹角的余弦值为 。
13.在(x – 1)(x + 1)5的展开式中x4的系数是________(用数字作答)
12.若对任意 ,(
,(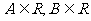 )有唯一确定的
)有唯一确定的 与之对应,则称
与之对应,则称 为关于
为关于 的二元函数。现定义满足下列性质的二元函数
的二元函数。现定义满足下列性质的二元函数 为关于实数
为关于实数 的广义“距离”:(1)非负性:
的广义“距离”:(1)非负性: ,当且仅当
,当且仅当 时取等号; (2)对称性:
时取等号; (2)对称性: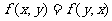 ; (3)三角形不等式:
; (3)三角形不等式: 对任意的实数
对任意的实数 均成立.今给出三个二元函数,①
均成立.今给出三个二元函数,① ;②
;② ;③
;③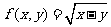 .能够成为关于的
.能够成为关于的 的广义“距离”的是 ( )
的广义“距离”的是 ( )
A.① B.①② C.①③ D.②③
11.设△ 是等腰三角形,
是等腰三角形, ,则以
,则以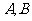 为焦点且过点
为焦点且过点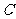 的双曲线的离心率为 ( )
的双曲线的离心率为 ( )
A. B.
B.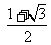 C .
C . D.
D.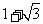
10.已知 是函数
是函数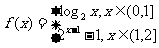 的反函数,则
的反函数,则 的值是 ( )
的值是 ( )
A.0 B. C.
C. D.1
D.1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com