
1.设全集U为实数集R,集合 ,则
,则
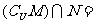 ( )
( )
A. B.
B. C.
C. D.
D.
2.对一切正整数 ,若不等式
,若不等式 恒成立,求
恒成立,求 的最小值.
的最小值.
1.求极限 ;
;
22.(本小题满分14分)
已知数列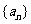 中,
中, ,且当
,且当 时,
时,
(I)求数列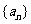 的通项公式;
的通项公式;
(Ⅱ)记
21.(本小题满分12分)

在平面直角坐标系 中,
中, 的斜边
的斜边 恰在
恰在 轴上,点
轴上,点 ,且
,且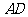 为
为 边上的高.
边上的高.

(I)求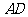 中点
中点 的轨迹方程;
的轨迹方程;
(Ⅱ)若一直线与(I)中 的轨迹交于两不同点
的轨迹交于两不同点 ,且线段
,且线段 恰以点
恰以点 为中点,求直线
为中点,求直线 的方程;
的方程;
(Ⅲ)若过点(1,0)的直线 与(I)中
与(I)中 的轨迹交于两不同点
的轨迹交于两不同点 试问在
试问在 轴上是否存在定点
轴上是否存在定点 ,使
,使 恒为定值
恒为定值 ?若存在,求出点
?若存在,求出点 的坐标及实数
的坐标及实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
20.
 (本小题满分12分)
(本小题满分12分)

已知函数


(I)当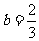 时,若函数
时,若函数 为
为 上的连续函数,求
上的连续函数,求 的单调区间;
的单调区间;
(Ⅱ)当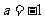 时,若对任意
时,若对任意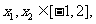 不等式
不等式 恒成立,求实数
恒成立,求实数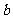 的取值范围.
的取值范围.
19.(本小题满分12分)

质检部门将对12个厂家生产的婴幼儿奶粉进行质量抽检,若被抽检厂家的奶粉经检验合格,则该厂家的奶粉即可投放市场;若检验不合格,则该厂家的奶粉将不能投放市场且作废品处理。假定这12个厂家中只有2个厂家的奶粉存在质量问题(即检验不能合格),但不知道是哪两个厂家的奶粉.

(I)从中任意选取3个厂家的奶粉进行检验,求至少有2个厂家的奶粉检验合格的概率;
(Ⅱ)每次从中任意抽取一个厂家的奶粉进行检验(抽检不重复),记首次抽检到合格奶粉时已经检验出奶粉存在质量问题的厂家个数为随即变量 ,求
,求 的分布列及数学期望.
的分布列及数学期望.

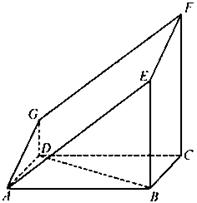
18.(本小题满分12分)

如图的多面体是直平行六面体 经平面
经平面 所截后得到的图形,其中
所截后得到的图形,其中 .
.

(I)求证: ;
;

(Ⅱ)求平面 与平面
与平面 所成锐二面角的大小;
所成锐二面角的大小;

(Ⅲ)求点C到平面 的距离
的距离



17.(本小题满分12分)

已知函数 .
.

(I)求 的值;
的值;

(II)若


 的值
的值

15.若关于 的方程
的方程 在[0,2]上有两个不同实数解,则实数
在[0,2]上有两个不同实数解,则实数 的取值范围是__________________.
的取值范围是__________________.

|
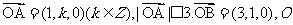 为坐标原点,给出以下结论:①以
为坐标原点,给出以下结论:①以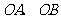 为邻边的平行四边形
为邻边的平行四边形 中,当且仅当
中,当且仅当 时,
时, 取得最小值;②当
取得最小值;②当 时,到
时,到 和点
和点 等距离的动点
等距离的动点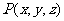 的轨迹方程为
的轨迹方程为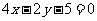 ,其轨迹是一条直线;③若
,其轨迹是一条直线;③若 则三棱锥
则三棱锥 体积的最大值为
体积的最大值为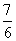 ;④若
;④若 =(0,0,1),则三棱锥
=(0,0,1),则三棱锥 各个面都为直角三角形的概率为
各个面都为直角三角形的概率为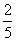 .
.

其中,所有正确结论的序号应是_____________________.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com