
5.设随机变量ξ服从正态分布 = ( )
= ( )
A.p B.-p C. D.
D.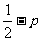
4.直线 的位置关系是( )
的位置关系是( )
A.相离 B.相切 C.相交 D.不能确定
3.已知等差数列 = ( )
= ( )
A.1 B.2 C. D.3
D.3
2.“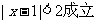 ”是“
”是“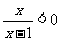 成立”的 ( )
成立”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
1.复数: = ( )
= ( )
A.0 B.2 C. D.
D.
21.本题共有(1)、)(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分。如果多作,则以所做的前2题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵 。
。
(i)求出矩阵A的逆矩阵A-1;
(ii)A决定的线性变换A将哪一个点变换到点(3,1)?
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在直角坐标系xOy中,已知曲线C1的参数方程是 现以原点O为极点,x轴的正半轴为极轴,建立极坐标系数。
现以原点O为极点,x轴的正半轴为极轴,建立极坐标系数。
(i)写出曲线C1的极坐标方程;
(ii)曲线C2的极坐标方程是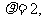 求曲线C2与曲线C1的交点的极坐标。
求曲线C2与曲线C1的交点的极坐标。
(3)(本小题满分7分)选修4-5:不等式选讲
(i)已知:a、b、 ;
;
(ii)某长方体从一个顶点出发的三条棱长之和等于3,求其对角线长的最小值。
20.(本小题满分14分)
设函数
(I)研究函数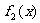 的单调性;
的单调性;
(II)比较 与0的大小,并证明你的结论;
与0的大小,并证明你的结论;
(III)判断关于x的方程 的实数解的个数,并加以证明。
的实数解的个数,并加以证明。
19.(本小题满分13分)
如图,已知A、B为椭圆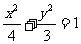 的左右两个顶点,F为椭圆的右焦点,P为椭圆上异于A、B点的任意一点,直线AP、BP分别交直线
的左右两个顶点,F为椭圆的右焦点,P为椭圆上异于A、B点的任意一点,直线AP、BP分别交直线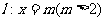 于M、N点,l交x轴于C点。
于M、N点,l交x轴于C点。

(I)当PF//l时,求直线AM的方程;
(II)是否存在m值使得以MN为直径的圆过F点,若存在,请加以证明,若不存在,请说明理由。
(III)对任意给定的m值,求△MFN面积的最小值。
18.(本小题满分13分)
在全球金融风暴的背景下,某政府机构调查了某地工薪阶层10000人的月工资收入,并把调查结果画成如图所示的频率分布直方图,请将频率当作概率解答以下问题。

(I)为了了解工薪阶层对月工资收入的满意程度,要用分层抽样方法从所调查的10000人中抽出100人作电话询访,则在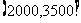 (元)月工资收入段应抽出多少人?
(元)月工资收入段应抽出多少人?
(II)为刺激消费,政府计划给该地所有工薪阶层的人无偿发放购物消费券,方法如下:月工资不多于2000元的每人可领取5000元的消费券,月工资在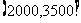 (元)间的每人可领取2000元的消费券,月工资多于3500元的每人可领取1000元的消费券。用随机变量ξ表示该地某一工薪阶层的人可领取的消费券金额,求ξ的分布列与期望值。
(元)间的每人可领取2000元的消费券,月工资多于3500元的每人可领取1000元的消费券。用随机变量ξ表示该地某一工薪阶层的人可领取的消费券金额,求ξ的分布列与期望值。
17.(本小题满分13分)
某长方体截去一个三棱锥后,形成的几何体的平面展开图的一部分如图(1-1)所示。

(I)请在图(1-2)上补画出该几何体的直观图,并求出被截去的三棱锥的体积;
(II)在该几何体的直观图中连结CD′,求证:CD′⊥AF;
(III)在该几何体中求平面AFG与平面ABCD所成的锐二面角的余弦值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com