
18.(本小题满分13分)
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD= ,AE、CF都与平面ABCD垂直,AE=1,CF=2。
,AE、CF都与平面ABCD垂直,AE=1,CF=2。
(Ⅰ)求二面角B-AF-D的大小;
(Ⅱ)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积。

17.(本小题满分12分)
某地有A、B、C、D四个人先后感染了甲型H1N1流感,其中只有A到过疫区,B肯定是受A感染的,对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率是 ,同样也假定D受A、B和C感染的概率都是
,同样也假定D受A、B和C感染的概率都是 ,在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量,写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
,在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量,写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
16.(本小题满分12分)
在 ABC中,
ABC中,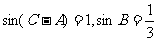
(I)求sinA的值;
(II)设AC= ,求
,求 ABC的面积
ABC的面积
15.对于四面体ABCD,下列命题正确的是_________(写出所有正确命题的编号)。
①相对棱AB与CD所在的直线是异面;
②由顶点A作四面体的高,其垂足是 BCD的三条高线的交点;
BCD的三条高线的交点;
③若分别作 ABC和
ABC和 ABD的边AB上的高,则这两条高所在的直线异面;
ABD的边AB上的高,则这两条高所在的直线异面;
④分别作三组相对棱中点的连线,所得的三条线段相交于一点。
⑤最长棱必有某个端点,由它引出的两条棱的长度之和大于最长棱。
14.给定两个长度为1的平面向量 和
和 ,它们的夹角为120°,如图所示,点C在以O为圆心的圆弧
,它们的夹角为120°,如图所示,点C在以O为圆心的圆弧 上变动,若
上变动,若 ,其中
,其中 ,则
,则 的最大值是________
的最大值是________

13.程序框图(即算法流程图)如图所示,其输出结果是_______

12.以直角坐标系的原点为极点, 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线的极坐标方程为
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线的极坐标方程为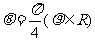 ,它与曲线
,它与曲线 ,(
,(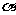 为参数)相交于两点A和B,则|AB|=________
为参数)相交于两点A和B,则|AB|=________
11.若随机变量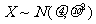 ,则
,则 =_______
=_______
10.考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6上点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于
A. B.
B. C.
C. D.
D.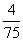
第Ⅱ卷(非选择题 共100分)
9.已知函数 在R上满足
在R上满足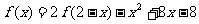 ,则曲线
,则曲线 在点
在点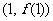 处的切线方程是
处的切线方程是
A. B.
B.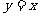 C.
C.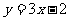 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com