3．长方体的对角线长度是，若长方体的8个顶点都在同一个球面上，则这个球的表面积是　　　　　　　　　　　 (　　 )

　　　 A．　　　　　　 B．　　　　　　 C．　　　　　　　　　 D．

2．若的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．3　　　　　　　　　　　　 B．-3　　　　　　　　　　 C．　　　　　　　　　　　 D．-

1．已知集合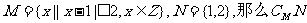等于　　　　　　　　　　　 (　　 )

　　　 A．{1，2}　　　　　　　 B．{-1，0，3}　　　 C．{0，3}　　　　　　　 D．{-1，0，1}

24．(本小题10分)选修4－5：不等式选讲

已知函数。

(Ⅰ)作出函数的图像；(Ⅱ)解不等式。

23．(本小题10分)选修4－4：坐标系与参数方程

已知曲线C₁：，曲线C₂：。

(Ⅰ)指出C₁，C₂各是什么曲线，并说明C₁与C₂公共点的个数；

(Ⅱ)若把C₁，C₂上各点的纵坐标都压缩为原来的一半，分别得到曲线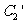，。写出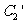，的参数方程。与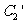公共点的个数和C₁与C₂公共点的个数是否相同？说明你的理由。

22．(本小题10分)选修4－1：几何证明选讲

从⊙O外一点P向圆引两条切线PA、PB和割线PCD。从A点作弦AE平行于CD，结BE交CD于F。求证：BE平分CD。

21．(本小题12分)

已知菱形的顶点在椭圆上，对角线所在直线的斜率为1．

(Ⅰ)当直线过点时，求直线的方程；

(Ⅱ)当时，求菱形面积的最大值．

请考生在第22、23、24题中任选一题做答，如果多做，则按所做的第一题记分。

20．(本小题12分)

水库的蓄水量随时间而变化，现用t表示时间，以月为单位，年初为起点，根据历年数据，某水库的蓄水量(单位：亿立方米)关于t的近似函数关系式为

V(t)=

(Ⅰ)该水库的蓄水量小于50的时期称为枯水期，以i－1＜t＜i表示第i月份(i=1,2,…,12),问一年内哪几个月份是枯水期？

(Ⅱ)求一年内该水库的最大蓄水量(取e=2.7计算).

19．(本小题12分)

在数列中，，。

(Ⅰ)求的通项公式；

(Ⅱ)令，求数列的前项和。

(Ⅲ)求数列的前项和。

18．(本小题12分)

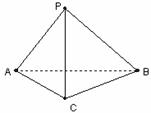
如图，在三棱锥中，，，，．

(Ⅰ)求证：；

(Ⅱ)求二面角的余弦值；

(Ⅲ)求点到平面的距离．