
20.(本小题满分14分)
已知函数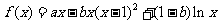 在x=1处有极值
在x=1处有极值
(Ⅰ)求a,b的关系式;
(Ⅱ)若b=0,函数 在
在 的最大值为2,求m的值;
的最大值为2,求m的值;
(Ⅲ)若a=0,对任意的正实数t,记f(x)在 的最小值为M(t),当t变化时,求
的最小值为M(t),当t变化时,求 的最大值
的最大值
19.(本小题满分13分)
已知椭圆C: 的离心率e=
的离心率e= ,点P为椭圆C上的任意一点,且点P到椭圆C的两个焦点的距离之和为4. 点M的坐标为(1,0).
,点P为椭圆C上的任意一点,且点P到椭圆C的两个焦点的距离之和为4. 点M的坐标为(1,0).

(Ⅰ)求椭圆C的方程;
(Ⅱ)过点P作直线PQ垂直于x轴,交椭圆C于点Q,直线PM交椭圆C于点N。试问,当点P在椭圆上运动时,直线QN是否恒经过定点S?若是,请求出点S的坐标,若不是,请说明理由.
18.(本小题满分13分)
已知三棱锥P- 中,PA,AB,AC两两垂直,M为PA上任意一点,D、E分别为AC,BC的中点,AB=3,AC=2,PA=4.
中,PA,AB,AC两两垂直,M为PA上任意一点,D、E分别为AC,BC的中点,AB=3,AC=2,PA=4.

(Ⅰ)求证:DE⊥平面PAC;
(Ⅱ)设平面MDE与平面PAB所成的角为θ(0°<θ<90°),试确定点M的位置,使得角θ为60°.
17.(本小题满分13分)
2008年5月12日四川省汶川发生8.0级地震,通往灾区的道路全部中断。5月12日晚,抗震救灾指挥部决定从水路(一支队伍),陆路(东南西北四个方向各一支队伍),空中(一支队伍)同时向灾区挺进.已知在5月13日,从水路抵达灾区的概率是 ,从空中抵达灾区的概率是
,从空中抵达灾区的概率是 ,从陆路每个方向抵达灾区的概率都是
,从陆路每个方向抵达灾区的概率都是 .
.
(Ⅰ)求在5月13日从水路或空中有队伍抵达灾区(即从水路和空中至少有一支队伍抵达灾区)的概率;
(Ⅱ)求在5月13日至少有4支队伍抵达灾区的期望.
16.(本小题满分13分)
已知函数 的部分图象如下图所示.
的部分图象如下图所示.

(Ⅰ)求函数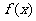 的解析式;
的解析式;
(Ⅱ)令函数 ,求函数
,求函数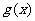 的单调递增区间.
的单调递增区间.
15.对于实数x,符号[x]表示不超过x的最大整数,例如 ,
, .已知
.已知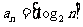 ,则满足
,则满足 的
的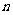 的最小正整数为 .
的最小正整数为 .
14.在△ABC中,角A、B、C所对的边分别为a、b、c,若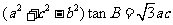 ,则角B的值为_________________.
,则角B的值为_________________.
13.圆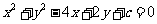 与y 轴交于A、B两点,其圆心为P, 若∠APB=
与y 轴交于A、B两点,其圆心为P, 若∠APB= ,则实数c=_____.
,则实数c=_____.
11. _____ _____.
_____ _____.
|
 满足线性约束条件
满足线性约束条件 目标函数
目标函数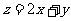 的最大值为 。
的最大值为 。10.对于在区间[a,b]上有意义的两个函数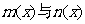 ,如果对于区间[a,b]中的任意x均有
,如果对于区间[a,b]中的任意x均有 ,则称
,则称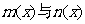 在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数
在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数 与
与 在区间[a,b]上是“密切函数”,则密切区间为 ( )
在区间[a,b]上是“密切函数”,则密切区间为 ( )
A.[3,4] B.[2,4] C.[2,3] D.[1,4]
第Ⅱ卷 (非选择题共100分)
本卷包括必答题和选答题两部分。第11题--第20题为必答题,每个试题考生都必须作答;第21(1)、(2)、(3)题为选考题,请考生根据要求选答.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com