
1.若等差数列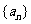 的前5项和
的前5项和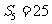 ,且
,且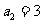 ,则
,则
A.12 B.13 C.14 D.15
20.(本小题共13分)
对于各项均为正数且各有m项的数列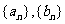 ,按如下方法定义数列
,按如下方法定义数列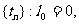
 的“并和”为
的“并和”为
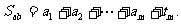
(I)若m=3,数列 为3,7,2,数列
为3,7,2,数列 为5,4,6,试求出t1、t2、t3的值以及数列
为5,4,6,试求出t1、t2、t3的值以及数列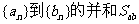 ;
;
(II)若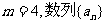 为3,2,3,4,数列
为3,2,3,4,数列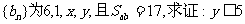 ;
;
(III)若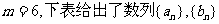 ;
;
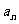 |
7 |
9 |
3 |
13 |
6 |
5 |
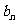 |
4 |
12 |
1 |
11 |
8 |
10 |
|
19.(本小题共14分)
已知椭圆 的左、右焦点分别为F1、F2,短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形.
的左、右焦点分别为F1、F2,短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形.
(I)求椭圆的方程;
(II)若C、D分别是椭圆长轴的左、右端点,动点M满足MD⊥CD,连结CM,交椭圆于点P,证明: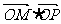 为定值;
为定值;
(III)在(II)的条件,试问x轴上是否存在异于点C的定点Q,使得以MP为直径的圆恒过直线DP,MQ的交点,若存在,求出点Q的坐标;若不存在,说明理由.
18.(本小题共13分)
3名志愿者在10月1号至10月5号期间参加社区服务工作.
(I)若每名志愿者在5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志原者恰好连续3天参加社区服务工作的概率;
(II)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记ξ表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量ξ的分布列.
17.(本小题共14分)
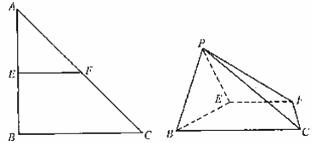
如图,在Rt△ABC中,AB=BC=4,点E、F分别在线段AB、AC上,且EF//BC,将△AEF沿EF折起到△PEF的位置,使得二面角P-EF-B的大小为60°.
(I)求证:EF⊥PB;
(II)当点E为线段AB的中点时,求PC与平面BCFE所成角的大小;
(III)求四棱锥P-EFCB体积的最大值.
16.(本小题共13分)
已知函数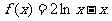
(I)写出函数 的定义域,并求其单调区间;
的定义域,并求其单调区间;
(II)已知曲线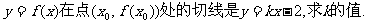
15.(本小题共13分)
在△ABC中,角A、B、C所对的边分别为a、b、c,已知
(I)求c的值及△ABC的面积S;
(II)求
14.已知函数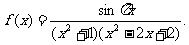
那么方程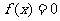 在区间[-100,100]上的根的个数是
;
在区间[-100,100]上的根的个数是
;
对于下列命题:①函数 是周期函数;②函数
是周期函数;②函数 既有最大值又有最小值;③函数
既有最大值又有最小值;③函数 的定义域是R,且其图象有对称轴;④对于任意
的定义域是R,且其图象有对称轴;④对于任意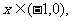 函数
函数 的导函数
的导函数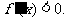 其中真命题的序号是
.(填写出所有真命题的序号)
其中真命题的序号是
.(填写出所有真命题的序号)
13.已知圆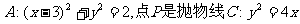 上的动点,过点P作圆A的两条切线,则两切线夹角的最大值为
.
上的动点,过点P作圆A的两条切线,则两切线夹角的最大值为
.
12.已知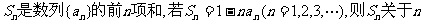 的表达式为
的表达式为
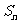 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com