18. (本小题满分12分)已知直三棱柱ABC-A₁B₁C₁中，A₁C与底面ABC所成的角为，AB=BC=，∠ABC=，设E、F分别是AB、A₁C的中点。

　(1)求证：BC⊥A₁E；

　(2)求证：EF∥平面BCC₁B₁；

　(3)求以EC为棱，B₁EC与BEC为面的二面角正切值。

17．(本小题满分12分)在△ABC中，tanA=,tanB=．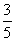

　(1)求角C的大小；

　(2)若AB边的长为，求BC边的长．

16．下列4个命题：

①在△ABC中，∠A>∠B是sinA>sinB的充要条件；

②若a>0,b>0，则a³+b³≥3ab²恒成立；

③对于函数f(x)=x²+mx+n,若f(a)>0，f(b)>0，则f(x)在(a，b)内至多有一个零点；

④y=f(x-2)的图象和y=f(2-x)的图象关于x=2对称。

其中正确命题序号________________。

15．已知函数f(x)=3x²+2x+1，若成立，则a=___________。

14．已知数列{a_n}中，a₁=,a_n+1=a_n+，则a_n=________．

13．设向量，，且与共线，则锐角为___________。

12．已知抛物线与双曲线有相同的焦点F，点A是两曲线的交点，且AF⊥x轴，则双曲线的离心率为　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

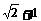　　　 A．　　　　　　　 B．　　　　　　　　 C．　　　　　　　　 D．

第Ⅱ卷(非选择题　共90分)

11．已知M={(x，y)|x+y≤6，x≥0，y≥0}，N={(x，y)|x≤4，y≥0，x-2y≥0}，若向区域M随机投一点P，则P落入区域N的概率为

　　　 A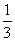．　　　　　　　　　　　 B．　　　　　　　　　　　 C．　　　　　　　　　　　 D．

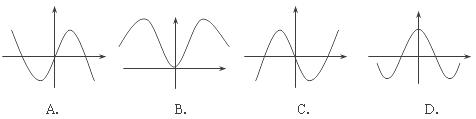
10．设曲线y=x²+1在其任一点(x，y)处切线斜率为g(x)，则函数y=g(x)•cosx的部分图象可以为

9．设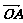=(1,-2)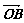，=(a,-1)，=(-b，0)，a>0,b>0,O为坐标原点，若A、B、C三点共线，则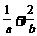的最小值是

　　　 A．2　　　　　　　　　　　　 B．4　　　　　　　　　　　　 C．6　　　　　　　　　　　　 D．8