3．用一些棱长是1cm的小正方体码放成一个几何体，图1为其俯视图，图2为其正视图，则这个几何体的体积最多是 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．6cm³　　　 B．7cm³ 　　　　　C．8cm³ 　　　　　　D．9cm³

2．△ABC中，BC=2，角B=，当△ABC的面积等于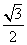时，sinC=　　　　　　　　　　　 (　　 )

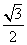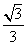　　　 A．　　　 　　　　 B．　　　 　　　　　　 C．　　 　　　　　　　 D．

1．已知全集U={-1，0，l，2}，集合A={-1，2}，B={0，2}，则=　　　　 (　　 )

　 　　 A．{0}　 　　　　　　　　 B．{2}　　　 　　　　　 C．{0，1，2}　 　　　　 D．

21．(本小题满分13 分)

设且为自然对数的底数，函数f(x)

　 (1)求证：当时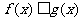，对一切非负实数x恒成立；

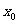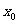　 (2)对于(0，1)内的任意常数a，是否存在与a 有关的正常数，使得成立？如果存在，求出一个符合条件的；否则说明理由.

20．(本小题满分13 分)

椭圆的离心率为，右准线方程为，左、右焦点分别为F₁，F₂ .

　 (1)求椭圆C 的方程

　 (2)若直线与以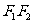为直径的圆相切并与椭圆C 交于A，B 两点，

且(O为坐标原点)，当时，求△AOB 面积的取值范围.

19．(本小题满分13 分)

某地区发生流行性病毒感染，居住在该地区的居民必须服用一种药物预防，规定每人每天早晚八时各服用一片，现知该药片每片含药量220 毫克. 若人的肾脏每12 小时从体内滤出这种药的60%，在体内的残留量超过386 毫克(含386 毫克)，就将产生副作用.

　 (1)某人上午八时第一次服药，问到第二天上午八时服完药时，这种药在人体内还残留多少？

　 (2)长期服用这种药的人会不会产生副作用？

18．(本小题满分12 分)

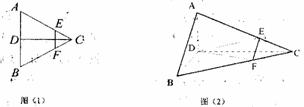
已知如图(1)，正三角形ABC 的边长为2a，CD 是AB 边上的高，E、F分别是AC 和BC 边上的点，且满足，现将△ABC 沿CD 翻折成直二面角A-DC-B,如图(2).

　 (1)试判断翻折后直线AB 与平面DEF的位置关系，并说明理由；

　 (2)求二面角B-AC-D 的大小；

　 (3)若异面直线AB 与DE 所成角的余弦值为，求k 的值.

17．(本小题满分12 分)在A，B 两只口袋中均有2 个红球和2 个白球，先从A 袋中任取2 个球转放到B 袋中，再从B 袋任取一个球转放到A 袋中，结果A 袋中恰有个红球.

　 (1)求=1 时的概率；

　 (2)求随机变量的分布列及期望.

16．(本小题满分12 分)

已知△ABC 各顶点的直角坐标为A(-1，0)、B(1，0)、C(m，)．

　 (2)若|CA| > |CB| ，且的值．

15．对于任意的正整数k，用g(k)表示k 的最大奇因数，例如：…，记则(i)当时，的关系是___________；(ii)=___________.