
22.(本小题满分14分)正方形ACDE所在的平面与平面ABC垂直,M是CE与AD的交点,AC⊥BC,且AC=BC.

(1)求证:AM⊥平面EBC;
(2)求直线AB与平面EBC所成角的大小;
(3)求二面角A-EB-C的大小.
21.(本小题满分12分)某公园有甲乙两个相邻的景点,原拟定甲景点内有2个A班的同学和2个B班的同学;乙景点内有2个A班的同学和3个B班的同学,后由于某种原因甲乙两景点各有一个同学交换景点观光.
(1)求甲景点恰有2个A班的同学的概率;
(2)求甲景点A班的同学数X的分布列及期望.
20.(本小题满分12分)已知 的展开式中奇数项的二项式系数之和比
的展开式中奇数项的二项式系数之和比 的展开式中偶数项的二项式系数之和大120,求:
的展开式中偶数项的二项式系数之和大120,求:
(1)n的值;
(2)(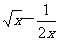 )
)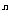 的展开式的中间项.
的展开式的中间项.
19.(本小题满分12分)一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点)
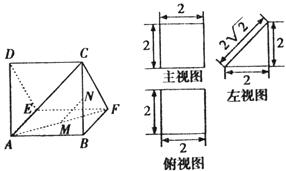
(1)求证:MN∥平面CDEF;
(2)求四棱锥A-CDEF的体积.
18.(本小题满分12分)甲、乙两队进行排球比赛,已知在一局比赛中甲队胜的概率为 ,没有平局,求:
,没有平局,求:
(1)若进行三局比赛,乙恰好获胜两局的概率是多少?
(2)若进行三局二胜制比赛,甲获胜的概率是多少?
17.(本小题满分12分)如图所示,平行六面体ABCD- 中,底面ABCD是边长为a的正方形,侧棱
中,底面ABCD是边长为a的正方形,侧棱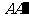 的长为b,且
的长为b,且 和AB与AD的夹角都等于120°.
和AB与AD的夹角都等于120°.

求 .
.
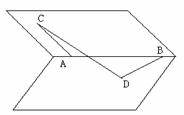
16.如图所示,在45°的二面角α-l-β的棱上有两点A、B,点C、D分别在α、β内,且AC⊥AB、∠ABD=45°,AC=BD=BA=1,则CD的长度是 。
15.已知分布列为
|
ξ |
-1 |
0 |
1 |
|
P |
 |
 |
a |
则
14.5名乒乓球队员中有2名老队员和3名新队员,现从中选出3名队员参加团体比赛,则入选的3名队员中至少有一名老队员的不同选法有 种。
13.在各棱长都等于1的正四面体OABC中,若点P满足 =x
=x +y
+y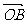 +z
+z (x+y+z=1),则
(x+y+z=1),则 的最小值为
。
的最小值为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com