2．抛物线的焦点坐标是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A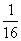．(，0)　　　　　 B．(0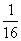，)　　　　　 C．(0，1)　　　　　　　 D．(1，0)

1．设集合A={-1，0，1，2}，B=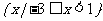，则A∩B　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．{-1，0，1}　　　　 B．{-1，0}　　　　　　　 C． D．

20．(本小题满分13分)

　　　 已知函数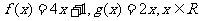，数列{a_n}，{b_n}，{c_n}满足条件：a₁=1，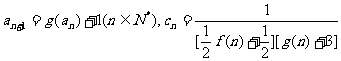

　 (Ⅰ)求数列{a_n}的通项公式；

　 (Ⅱ)求数列{b_n}的前n项和为T_n，并求使得T_n＞对任意n∈N*都成立的最大正整数m；

　 (Ⅲ)求证：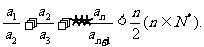

19．(本小题满分14分)

　　　 已知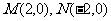，动点P满足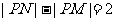，点P的轨迹为W，过点M的直线与轨迹W交于A，B两点。

　 (Ⅱ)若，求直线AB斜率k的值，并判断以线段AB为直径的圆与直线的位置关系，并说明理由。

18．(本小题满分13分)

　　　 某学校进行交通安全教育，设计了如下游戏，如图，一辆车模要直行通过十字路口，此时前方交通灯为红灯，且该车模前面已有4辆车模依次在同一车道上排队等候(该车道只可以直行或左转行驶)。已知每辆车模直行的概率是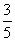，左转行驶的概率是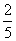，该路口红绿灯转换间隔时间均为1分钟，假设该车道上一辆直行去东向的车模驶出停车线需要10秒钟，一辆左转去北向的车模驶出停车线需要20秒钟，求：

　 (Ⅰ)前4辆车模中恰有2辆车左转行驶的概率；

　 (Ⅱ)该车模在第一次绿灯亮起时的1分钟内通过该路口的概率(汽车驶出停车线就算通过路口)。

17．(本小题满分13分)

　　　 已知函数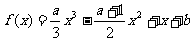，其中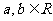

　 (Ⅰ)若曲线在点P(2，f(2))处的切线方程为，求函数的解析式

　 (Ⅱ)当a＞0时，谈论函数的单调性。

16．(本小题满分14分)

　　　 在直四棱柱ABCD-A₁B₁C₁D₁中，已知AB∥CD，AB=AD=1，D₁D=CD=2，AB⊥AD。

　 (Ⅰ)求证：BC⊥D₁DB；

　 (Ⅱ)求D₁B与平面D₁DCC₁所成角的大小；

15．(本小题满分13分)

　　　 在△ABC中，角A、B、C所对的边分别为a，b，c，已知向量m=(a，3b-c)，n=(cosA，cosC)，满足m∥n。

　 (Ⅰ)求cosA的大小；

　 (Ⅱ)求的值。

14．对于集合N={1，2，3，…，n}的每一个非空子集，定义一个“交替和”如下：按照递

13．已知点P为椭圆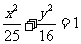上的动点，F₁、F₂为椭圆的左、右焦点，则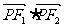的最小值为　　　　　 ，此时P点的坐标为　　　　　　 。