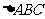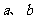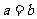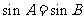2．在中，分别是角A、B所对的边，条件“”是使“”成立的

A．充分不必要条件　　　　　　　 B．必要不充分条件

C．充要条件　　　 　　　　　　　D．既不充分也不必要条件

1．已知集合，则=

A．　　　　 　　　　　　　　 B．　　　　 　　 C．　　　　 D．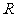

20．(本小题满分13分)

已知函数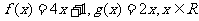，数列{a_n}，{b_n}，{c_n}满足条件：a₁=1，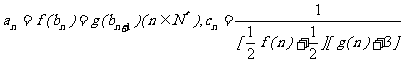

　 (Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)求数列{c_n}的前n项和为T_n，并求使得T_n＞对任意n∈N*都成立的最大正整数m；

　 (Ⅲ)求证：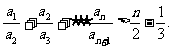

19．(本小题满分14分)

已知动圆P过点N(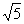，0)并且与圆M：相外切，动圆圆心P的轨迹为W，轨迹W与x轴的交点为D。

　 (Ⅰ)求轨迹W的方程；

(Ⅱ)设直线l过点(m，0)(m＞2)且与轨迹W有两个不同的交点A，B，求直线l的斜率k的取值范围；

(Ⅲ)在(Ⅱ)的条件下，若，证明直线l过定点，并求出这个定点的坐标。

　　　 ①按“单打、双打、单打”顺序进行三盘比赛；

　　　 ②代表队中每名队员至少参加一盘比赛，但不得参加两盘单打比赛；

　　　 ③先胜两盘的队获胜，比赛结束。已知每盘比赛双方胜出的概率均为。

　 (Ⅰ)根据比赛规则，高三(1)班代表队共可排出多少种不同的出场阵容；

　 (Ⅱ)高三(1)班代表队连胜两盘的概率为多少？

　 (Ⅲ)设高三(1)班代表队获胜的盘数为，求的分布列和数学期望。

18．(本小题满分13分)

　　　 已知函数

　 (Ⅰ)若曲线在点P(1，f(1))处的切线垂直于y轴，求实数a的值；

17．(本小题满分13分)

16．(本小题满分14分)

　　　 在直四棱柱ABCD-A₁B₁C₁D₁中，已知AB∥CD，AB=AD=1，D₁D=CD=2，AB⊥AD。

　 (Ⅰ)求证：BC⊥D₁DB；

　 (Ⅱ)求D₁B与平面D₁DCC₁所成角的大小；

(Ⅲ)在BB₁上是否存在一点F，使F到平面D₁BC的距离为，则指出该点的位置；若不存在，请说明理由。

15．(本小题满分13分)

在△ABC中，角A、B、C所对的边分别为A，B，C，已知向量m=(a，3b-c)，n=(cosA，cosC)，满足m∥n。

　 (Ⅰ)求cosA的大小；

　 (Ⅱ)求的值。

14．对于集合N={1，2，3，…，N}的每一个非空子集，定义一个“交替和”如下：按照递减的次序重新排列该子集，然后从最大数开始交替地减、加后面的数。例如集合{1，2，4，6，9}的交替和是9-6+4-2+1=6，集合{5}的交替和为5，当集合N中的n=2，集合N={1，2}的所有非空子集为{1}，{2}，{1，2}，则它的“交替和”的总和S₂=1+2+(2-1)=4，请你尝试对n=3、n=4的情况，计算它的“交替和”的总和S₃、S₄，并根据其结果猜测集合N={1，2，3，…,n}的每一个非空子集的“交替和”的总和S_n=　　　　　　　 。

13．已知F(C，0)是椭圆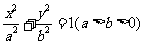的右焦点，以坐标原点O为圆心，A为半径作圆P，过F垂直于x轴的直线与圆P交于A，B两点，过点A作圆P的切线交x轴于点M。若直线l过点M且垂直于x轴，则直线l的方程为　　　　　 ；若|OA|=|AM|，则椭圆的离心率等于　　　　　　　 。