
4.函数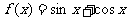 在点(0,
在点(0, )处的切线方程为
)处的切线方程为
A. B.
B. C.
C. 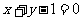 D.
D.
3.在等比数列{ }中,若
}中,若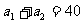 ,
,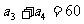 则
则
A.150 B.135 C.95 D.80
2.已知命题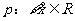 ,使
,使 ;命题
;命题 ,都有
,都有 。下列结论中正确的是
。下列结论中正确的是
A.命题“ ”是真命题 B.命题“
”是真命题 B.命题“ ”是真命题
”是真命题
C.命题“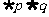 ”真命题 D.命题“
”真命题 D.命题“ ”是假命题
”是假命题
1.如果直线 与直线
与直线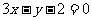 平行,那么实数
平行,那么实数 等于
等于
A.-3 B.-6 C.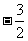 D.
D.
22.(本小题满分14分)
已知椭圆 的离心率
的离心率 ,其长轴长为4。
,其长轴长为4。
(Ⅰ)求椭圆的方程;
(Ⅱ)若菱形ABCD的顶点A,C在椭圆 上,对角线BD所在直线的斜率为1。
上,对角线BD所在直线的斜率为1。
(1)当直线BD过点(0,1)时,求直线AC的方程;
(2)当∠ABD=30°时,求菱形ABCD面积的最大值。
21.(本小题满分12分)
如下图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°, ,EF=2。
,EF=2。
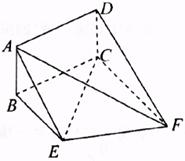
(Ⅰ)求证:AE∥平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为60°?
20.(本小题满分12分)
已知命题 :当
:当 时,
时, 恒成立。命题
恒成立。命题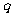 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线,若命题“
轴上的双曲线,若命题“ ”为假命题,求实数
”为假命题,求实数 的取值范围。
的取值范围。
19.(本小题满分12分)
已知圆C的方程为 。
。
(Ⅰ)若圆C的切线在 轴,
轴,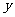 轴上的截距相等,求此切线的方程。
轴上的截距相等,求此切线的方程。
(Ⅱ)从圆C外一点P(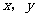 )向该圆引一条切线,切点为M,O为坐标原点,且有
)向该圆引一条切线,切点为M,O为坐标原点,且有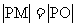 ,求P点的轨迹方程。
,求P点的轨迹方程。
18.(本小题满分12分)
从集合{-2,-1,0,1,2}任取两个不同数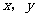 作为P点的坐标(
作为P点的坐标(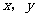 )。
)。
(Ⅰ)写出这个试验的所有基本事件;
(Ⅱ)求点P落在坐标轴上的概率;
(Ⅲ)求点P落在圆 外的概率。
外的概率。
17.(本小题满分12分)
已知函数 ,设计一个算法,计算并输出
,设计一个算法,计算并输出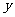 值,画出该算法的程序框图。
值,画出该算法的程序框图。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com