
20.(本小题满分13分)
已知函数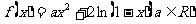 .
.
(Ⅰ)若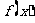 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)是否存在正实数 ,使得
,使得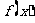 的导函数
的导函数 有最大值
有最大值 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
19.(本小题满分12分)
平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,-2),点C满足  、
、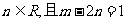 .
.
(Ⅰ)求点C的轨迹方程;
(Ⅱ)设点C的轨迹与双曲线 交于两点M、N,且以MN为直径的圆过原点,求证
交于两点M、N,且以MN为直径的圆过原点,求证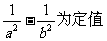 ;
;
(Ⅲ)在(Ⅱ)的条件下,若双曲线的离心率不大于 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
18.(本小题满分12分)
已知四棱锥  的底面是直角梯形,
的底面是直角梯形, ∥
∥ ,
, ,
, ,侧面
,侧面 底面
底面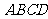 .
.

(Ⅰ)求证: ;
;
(Ⅱ)求二面角 的正切值.
的正切值.
17.(本小题满分12分)
某工厂规定,如果工人在一个季度里有1个月完成生产任务,可得奖金90元;如果有2个月完成生产任务,可得奖金210元;如果有3个月完成生产任务,可得奖金330元;如果工人三个月都未完成任务,则没有奖金.假设某工人每月完成任务与否是等可能的,求此工人在一个季度里所得奖金的期望.
16.(本小题满分12分)
设函数 ,其中向量
,其中向量 ,
, ,且
,且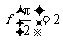 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求函数 在区间
在区间 上的最大值.
上的最大值.
15.已知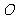 是△
是△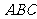 的外心,
的外心,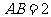 ,
, ,
,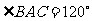 .设
.设 ,
, ,若
,若 ,则
,则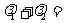 ______________.
______________.
14.如果在一周内(周一至周日)安排三所学校的学生参观某展览馆,每天最多只安排一所学校,要求甲学校连续参观两天,其余两所学校均只参观一天,那么不同的安排方法共有_____种.
13.数列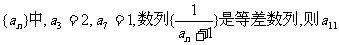 =
.
=
.
12.给出下列命题: ①垂直于同一直线的两条直线平行;②若一条直线垂直于两条平行线中的一条,则它垂直于另一条;③若一条直线与两条平行线中的一条相交,则它与另一条相交;④一条直线至多与两条异面直线中的一条相交.
其中正确命题的序号是____________ (写出所有正确命题的序号).
11.过点 的直线
的直线 与曲线
与曲线 :
: 相交于
相交于 两点,若点
两点,若点 是弦
是弦 的中点,则直线
的中点,则直线 的方程为______________________.
的方程为______________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com