
22.设函数 满足
满足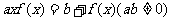 ,且
,且
(1)求函数 的解析式。
的解析式。
(2)若数列{ }的前n项和是
}的前n项和是 ,
,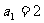 ,且
,且
( )求数列{
)求数列{ }的通项公式,写出推证过程。
}的通项公式,写出推证过程。
(3)若数列{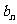 }满足
}满足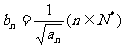 ,数列{
,数列{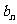 }的前n项和为
}的前n项和为 ,求证:
,求证:
 . (14分)
. (14分)
21.设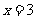 是函数
是函数 的一个极值点.(12分)
的一个极值点.(12分)
(1)求 与
与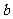 的关系式(用
的关系式(用 表示
表示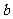 ),并求
),并求 的单调区间;
的单调区间;
(2)设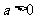 ,
, .若存在
.若存在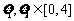 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.
20.某农产品去年各季度的市场价格如下表:(12分)
|
季 度 |
第一季度 |
第二季度 |
第三季度 |
第四季度 |
|
每担售价(单位:元) |
195.5 |
200.5 |
204.5 |
199.5 |
今年某公司计划按去年各季度市场价的“最佳近似值m”(m是与上表中各售价差的平方和取最小值的值)收购该种农产品,并按每100元纳税10元(又称征税率为10个百分点,计划可收购a万担,政府为了鼓励收购公司多收购这种农产品,决定将税率降低x个百分点,预测收购量可增加2x个百分点.
(1)根据题中条件填空,m= (元/担);
(2)写出税收y(万元)与x的函数关系式;
(3)若要使此项税收在税率调节后不少于原计划税收的83.2%,试确定x的取值范围.
19.如图,边长为2的正三角形ADE垂直于矩形ABCD所在平面,F是AB的中点,EC和平面ABCD成45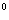 角.(1)求四棱锥E-AFCD的体积;(2)求二面角E-FC-D的大小;(3)求D到平面EFC的距离.(12分)
角.(1)求四棱锥E-AFCD的体积;(2)求二面角E-FC-D的大小;(3)求D到平面EFC的距离.(12分)

18.函数f(x)= 满足
满足
(1)若 ,求
,求 的最大值和最小值;
的最大值和最小值;
(2)若要得到 的图象,需将
的图象,需将 的图象作怎样的变化?
的图象作怎样的变化?
(3)若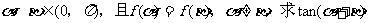 (12分)
(12分)
17.已知命题P:不等式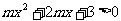 在R上恒成立;命题q:函数
在R上恒成立;命题q:函数 在区间[0,2]是增函数.求实数
在区间[0,2]是增函数.求实数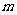 的取值范围,使“P或q”为真命题,“P且q”为假命题.(12分)
的取值范围,使“P或q”为真命题,“P且q”为假命题.(12分)
16.在平几中,直角三角形ABC中有性质:若 为斜边c上的高,a、b为直角边,则(1)
为斜边c上的高,a、b为直角边,则(1)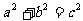 ,(2)
,(2) 。类比到立几中,直角三棱锥(三侧棱两两垂直)三侧棱长分别为a、b、c,三侧面面积分别为
。类比到立几中,直角三棱锥(三侧棱两两垂直)三侧棱长分别为a、b、c,三侧面面积分别为 ,底面上的高为h,底面面积为S,那么有类似于性质:(1)或(2)的等式为_________________________.(填一个即可)
,底面上的高为h,底面面积为S,那么有类似于性质:(1)或(2)的等式为_________________________.(填一个即可)
15.一个袋中装有5个白球5个黑球,现在做摸球有奖游戏。从中取5球,若5球同色,则获奖金50元;若仅有4个黑色球,则获奖金20元;若仅有1个黑色球,则获奖金5元;其余情况则付款10元。那么摸一次球获得奖金的期望是_______________。
14.若三个正数a、b、c成等比数列,且有a,1-b,c成等差数列,则实数b的取值范围是 .
13.若函数f(x)=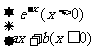 在x=0处连续,则b=_____________.
在x=0处连续,则b=_____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com