1．设集合=　　　　 。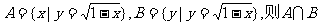

22．(本题满分14分)

已知　

　 (1)当a=2时，求函数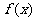的单调递增区间；

　 (2)若函数的取值范围；

　 (3)函数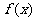是否为R上的单调函数，若是求出a的取值范围；若不是说明理由。

21．已知函数

　 (1)求

　 (2)是否存在实数m，n，同时满足下列条件：

　　　　 ①，②当的定义域为[n，m]时，值域为，若存在，求出m，n的值，若不存在，说明理由。

20．(本题满分12分)

　　 若函数

　 (1)求函数的解析式；

　 (2)若关于x的方程有三个零点，求实数k的取值范围。

19．如图，甲船以每小时海里的速度向正北方向航行，乙船按固定的方向匀速直线航行，当甲船位于A₁处时，乙船位于甲船的北偏西105°方向B₁的处，此时两船相距20海里，当甲船航行20分钟到达A₂处时，乙船航行到甲船的北偏西120°方向的B₂处，此时两船相距海里，问乙船每小时航行多少海里？

18．已知平面向量

　 (1)证明：；

　 (2)若存在不同时为零的实数k和t，使，试求的函数关系式；

　 (3)若上是增函数，试求k的取值范围。

17．已知A、B均为钝角，且，求A+B。

16．设函数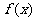的定义域为D，如果对于任意

　 (c为常数)成立，则称函数在D上均值为c，给出下列五个函数：

①，②，③，④，⑤

满足在其定义域上均值为2的所有函数的序号是　 　　　　　。

15．曲线处的切线方程与坐标轴围成的三角形面积是　　 　　　。

14．已知函数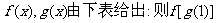的值为　 __；满足的值　　　　　 。

x	1	2	3
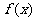	1	3	1
	3	2	1