
5.如果一个椭圆的长轴长是短轴长的两倍,那么这个椭圆的离心率为
A.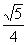 B.
B.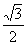 C.
C.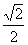 D.
D.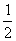
4.若 为一条直线,
为一条直线, 为三个互不重合的平面,给出下面三个命题:
为三个互不重合的平面,给出下面三个命题:
①  ②
②  ∥
∥
③  ∥
∥ .
.
其中正确的命题有
A.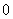 个
B.
个
B.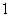 个
C.
个
C.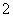 个
个
 D.
D.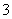 个
个
3.已知非零向量 与
与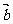 的夹角为
的夹角为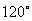 ,且
,且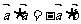 ,则
,则 的值为
的值为
A. 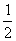 B.
B. C.
C.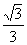 D.
D.
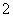
2.四名志愿者和他们帮助的两名老人排成一排照相,要求两名老人必须站在一起,则不同的排列方法为
A. B.
B. C.
C.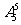 D.
D.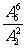
1.已知集合 ,且
,且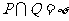 .那么
.那么 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D.
22.(本小题满分14分)
已知定义在R上的函数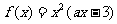 ,其中a为常数.
,其中a为常数.
(I)若x=1是函数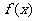 的一个极值点,求a的值;
的一个极值点,求a的值;
(II)若函数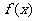 在区间(-1,0)上是增函数,求a的取值范围;
在区间(-1,0)上是增函数,求a的取值范围;
(III)若函数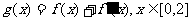 ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.
21.(本小题满分12分)
在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东 且与点A相距40
且与点A相距40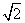 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东 +
+ (其中sin
(其中sin =
=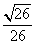 ,
, )且与点A相距10
)且与点A相距10 海里的位置C.
海里的位置C.
(I)求该船的行驶速度(单位:海里/小时);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
20.(本小题满分12分)
已知二次函数 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为 ,数列
,数列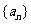 的前n项和为
的前n项和为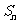 ,点
,点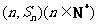 均在函数
均在函数 的图像上。
的图像上。
(Ⅰ)求数列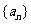 的通项公式;
的通项公式;
(Ⅱ)设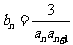 ,
,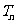 是数列
是数列 的前n项和,求使得
的前n项和,求使得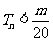 对所有
对所有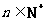 都成立的最小正整数m.
都成立的最小正整数m.
19.(本小题满分12分)
在矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC∩BD=G.
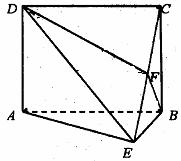
(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求证:AE//平面BFD;
(Ⅲ)求三棱锥C-BGF的体积.
18.(本小题满分12分)
已知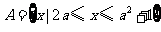 ,
,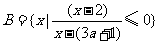 ,其中
,其中 .
.
(Ⅰ)当a=3时,求( ;
;
(Ⅱ)若命题p: ,q:
,q: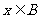 ,且p是q的充分不必要条件,求实数
,且p是q的充分不必要条件,求实数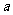 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com