
18.(12分)甲、乙两人玩轮流抛掷一对骰子的游戏,第一次由甲掷,第二次由乙掷,然后甲再掷,如此轮流下去……,规定先得到两颗骰子点数之和等于7的一方获胜,一旦决出胜负游戏便结束.
(1)求抛掷1次甲就获胜的概率;
(2)若限定每人最多掷两次,试比较游戏结束时甲获胜的可能性是否比乙更大?
17.(10分)已知向量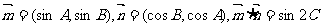 ,且A、B、C分别为△ABC的三边所对的角。
,且A、B、C分别为△ABC的三边所对的角。
(1)求角C的大小;
(2)若三边a、b、c成等差数列,且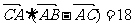 ,求边c的长。
,求边c的长。
16.如图1,一个正四棱柱形的密闭容器,其底部镶嵌了同底的正四棱锥形实心装饰块。容器内盛有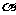 升水时,水面恰好经过正四棱锥的顶点P,如果将容器倒置,水面也恰好过点P(如图2)。有下面四个命题:
升水时,水面恰好经过正四棱锥的顶点P,如果将容器倒置,水面也恰好过点P(如图2)。有下面四个命题:
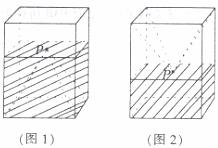
①正四棱锥的高等于正四棱柱高的一半;
②将容器侧面水平放置时,水面也恰好过点P;
③任意摆放该容器,当水面静止时,水面都恰好经过点P;
④若往容器再注入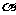 升水,则容器恰好能装满。
升水,则容器恰好能装满。
其中真命题的序号是 (把所有真命题的序号都写上)
15.已知F1、F2分别是椭圆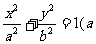 >
>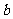 >0)的左、右两焦点,P是其右准线上纵坐标为
>0)的左、右两焦点,P是其右准线上纵坐标为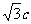 (c为半焦距)的点,若
(c为半焦距)的点,若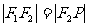 ,则该椭圆的离心率是 .
,则该椭圆的离心率是 .
14.已知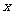 ,
,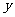 满足条件
满足条件 ,则
,则 的最小值为
.
的最小值为
.
13.若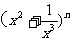 展开式的各项系数之和为32,则其展开式中的常数项是 .
展开式的各项系数之和为32,则其展开式中的常数项是 .
12.定义在R上的函数满足: ,当
,当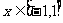 时,
时,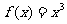 ,则
,则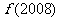 的值等于( )
的值等于( )
A.一1 B.1 C.0 D.2
第Ⅱ卷 (非选择题共90分)
11.已知O为△ABC内一点,且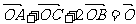 ,则△AOC与△ABC的面积之比是( )
,则△AOC与△ABC的面积之比是( )
A.1:2 B.1:3 C.2:3 D.1:1
10.函数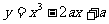 在(0,1)内有极小值,则实数
在(0,1)内有极小值,则实数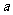 的取值范围是( )
的取值范围是( )
A.(0,3) B.(一∞,3) C.(0,1.5) D. (0,+∞)
9.某班级要从4名男生、2名女生中选派4人参加某次社会活动,如果要求至少有1名女生.那么不同的选派方法共有( )
A.48种 B.32种 C.28种 D.14种
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com