
19.(本小题满分12分)
如图: PA⊥平面ABCD,ABCD是矩形,PA=AB=1, AD= ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(Ⅰ)求三棱锥E-PAD的体积;
(Ⅱ)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅲ)证明:无论点E在边BC的何处,都有PE⊥AF.

18.(本小题满分12分)
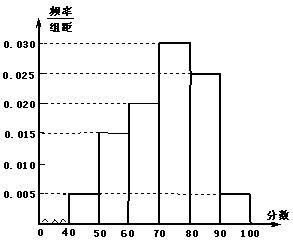
某校从高一年级期末考试的学生中抽出 名学生,其成绩(均为整数)的频率分布直方图如图所示:
名学生,其成绩(均为整数)的频率分布直方图如图所示:
(Ⅰ)估计这次考试的平均分;
(Ⅱ) 假设在[90,100]段的学生的成绩都不相同,且都在94分以上,现用简单随机抽样方法,从 这
这 个数中任取
个数中任取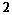 个数,求这
个数,求这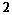 个数恰好是两个学生的成绩的概率.
个数恰好是两个学生的成绩的概率.
17.(本小题满分12分)
如图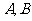 是单位圆
是单位圆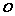 上的动点,且
上的动点,且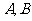 分别在第一,二象限.
分别在第一,二象限. 是圆与
是圆与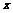 轴正半轴的交点,
轴正半轴的交点, 为正三角形. 若
为正三角形. 若 点的坐标为
点的坐标为 . 记
. 记 .
.
(Ⅰ)若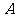 点的坐标为
点的坐标为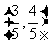 ,求
,求 的值;
的值;
(Ⅱ)求 的取值范围.
的取值范围.

16.如图,正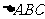 的中线
的中线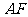 与中位线
与中位线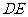 相交于
相交于 ,已知
,已知 是
是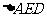 绕
绕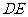 旋转过程中的一个图形,现给出下列四个命题:
旋转过程中的一个图形,现给出下列四个命题:
①动点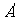 在平面
在平面 上的射影在线段
上的射影在线段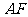 上; ②恒有平面
上; ②恒有平面 ;
;
③三棱锥 的体积有最大值;④异面直线
的体积有最大值;④异面直线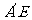 与
与 不可能垂直.
不可能垂直.
其中正确的命题的序号是 .

15.函数 的最小值为
.
的最小值为
.
14.已知函数 在区间(0,1)上是减函数,则实数a的取值范围是 .
在区间(0,1)上是减函数,则实数a的取值范围是 .
13.已知 若平面上的三点
若平面上的三点 共线,则
共线,则 .
.
12.定义在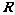 上的偶函数
上的偶函数 ,满足
,满足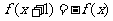 ,且
,且 在[-1,0]上是增函数,下列四个关于
在[-1,0]上是增函数,下列四个关于 的命题中:
的命题中:
① 是周期函数; ②
是周期函数; ② 在[0,1]上是减函数;
在[0,1]上是减函数;
③ 在[1,2]上是增函数; ④
在[1,2]上是增函数; ④ 的图象关于
的图象关于 对称;
对称;
其中正确命题的个数是 ( )
A.1个 B.2个 C.3个 D.4个
第II卷
本卷包括必考题和选考题两部分,第13题-第21题为必考题,每个试题考生都必须做答,第22,23,24题为选考题,考生根据要求做答.
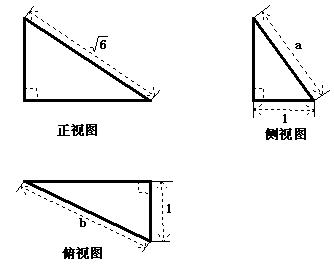
11.某几何体的三视图如图所示,当 取最大值时,这个几何体的体积为 ( )
取最大值时,这个几何体的体积为 ( )
A. B.
B.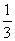 C.
C. D.
D.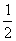
10.已知 ,则
,则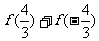 的值为 ( )
的值为 ( )
A.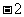 B.
B. C.1 D.2
C.1 D.2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com