
21.(本小题满分12分)
平面上有两个质点A(0,0),B(2,2)在某一时刻开始每隔1秒向上,下,左,右任一方向移动一个单位,已知质点A向左,右移动的概率都是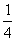 ,向上,下移动的概率分别为
,向上,下移动的概率分别为 ,质点B向四个方向移动的概率均为
,质点B向四个方向移动的概率均为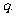
(1)求 和
和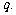 的值;
的值;
(2)试判断至少需要几秒,A,B能同时到达D(1,2),并求出在最短时间内同时到达的概率。
20.(本小题满分14分)
(文科)如图,直三棱柱ABC-A1B1C1中,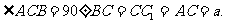
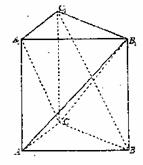
(I)求证: 平面AB1C;
平面AB1C;
(II)求二面角B-AB1-C的大小;
(III)求三棱锥A1-AB1C的体积。
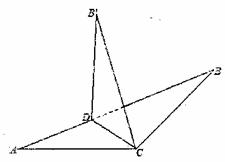
(理科)如图,在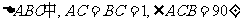 点D在斜边AB上,
点D在斜边AB上,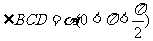 ,把
,把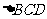 沿CD折起到
沿CD折起到 的位置,使平面
的位置,使平面 平面ACD。
平面ACD。
(I)求点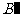 到平面ACD的距离(用
到平面ACD的距离(用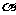 表示);
表示);
(II)求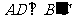 时,求三棱锥
时,求三棱锥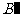 -ACD的体积;
-ACD的体积;
(III)当点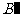 在平面ACD内的射影为线段CD的中点时,求异面直线AD与
在平面ACD内的射影为线段CD的中点时,求异面直线AD与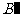 C所成角的余弦值。
C所成角的余弦值。
19.(本小题满分12分)
已知向量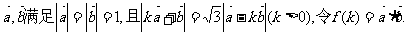
(I)求 的表达式;
的表达式;
(II)若函数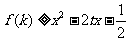 对任意的
对任意的 恒成立,求实数
恒成立,求实数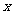 的取值范围。
的取值范围。
18.(本小题满分12分)
设函数 的最大值为M,最小正周期为
的最大值为M,最小正周期为
(I)求M,T的值及单调递增区间;
(II)10个互不相等的正数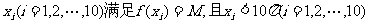
,求 的值。
的值。
17.(本小题满分12分)
求与直线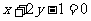 切于点A(1,0),且过点B(2,-3)的圆的方程。
切于点A(1,0),且过点B(2,-3)的圆的方程。
16.(文科)函数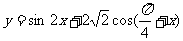 的最小值为
的最小值为
(理科)函数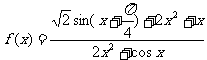 的最大值为M,最小值为
的最大值为M,最小值为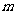 ,则M+
,则M+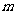 =
=
15.函数 的单调递增区间为
的单调递增区间为
14.某企业有高级工程师26人,普通技工104人,其他职员若干人,为了了解该企业员工的工资收入情况,若按分层抽样从该企业的所有员工中抽取56人进行调查,已知从其他职员中抽取了16人,则该企业共有员工 人。
13.函数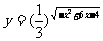 的值域为
的值域为
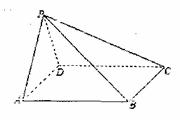
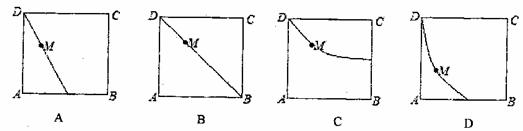
12.如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹为 ( )
第Ⅱ卷(非选择题 共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com