14．做一个容积为256L的方底无盖水箱，则它的高为___________时，最省材料。

13．若a、b、c成等比数列，a、x、b成等差数列，b、y、c成等差数列，则　 ；

22．(14分)已知函数f(x)＝的反函数f^－1(x)＝。

(1)求函数f(x)的解析式及定义域。

(2)若x＞0时，令f(x)＝f₁(x)，f_n(x)=f_n－1[f_n-1(x)](n∈N，且N≥2)

　　　　　　　 ①求f_n(x)并用数学归纳法证明。　　 ②证明f₁(x)+2f₂(x)+……+n f_n(x)＜4

20．设函数f(x)＝(1+x)²－ln (1+x²), (x＞－1)

　　　 ①若当x∈[－1，e－1]时，不等式f(x)＜m恒成立，求m的范围。

　　　 ②若关于x的方程f(x)＝x²+x+a在区间[0，2]上恰有两个相异实根，求a的取值范围。

21(12分)如图ABCD是边长2a的正方形铁板，剪掉四个阴影部分的小正方形沿虚线折叠

　　　 焊接成一个无盖长方体水箱。若水箱高度x与底面边长的比不超过常数k(k＞0)

　　　 (1)写出水箱容积V与x的函数表达式，并求定义域。

　　　 (2)当高度x为何值时，水箱容积V最大，并求出最大值。

19．(12分)假设从“神七”飞船带回的某植物种子每粒发芽概率都为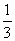，某研究所进行该种子发芽实验，每次实验用一粒种子，每次实验结果相互独立，若种子发芽则此次实验成功，若没发芽，则称此次实验失败。共进行四次实验，设∮表示四次实验成功次数与失败差的绝对值。

(1)求∮的数学期望。

(2)记事件A表示“不等式∮x²－∮x+1＞0”的解集为R，求事件A的发生概率。

18．(12分)已知f(x)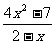＝，x∈[0，1]

　　　 (1)求f(x)的单调区间和值域。

　　　 (2)设a≥1，函数g(x)＝x³－3a²x－2a,x∈[0，1]，若对任意x₁∈[0，1]，总存在

　　　 　　 x₀∈[0,1]，使g(x₀)＝f(x₁)成立，求a的范围。

17．(12分)已知集合A＝{x|x²+3x+2＜0，B＝{x|x²－4ax+3a＜0若A∩B＝φ，求a的范围。

16．下列命题

　　　 ①f(x)在x＝x₀处连续是f(x)在x＝x₀处可导的必要非充分条件。

　　　 ②采用随机，系统，分层抽样，每个个体被抽取的概率都相同。

　　　 ③定义域A＝{x₁,x₂,x₃,x₄,x₅}到值域B＝{y₁，y₂，y₃}的不同映射有3⁵个。

　　　 ④若函数f(x)＞g(x)对任意x恒成立，则f(x)_min＞g(x)_max必成立。

　　　 为真命题的序号是　　　　　　　　 。

15．定义运算a*b= 则f(x)＝x²*(1－|x|)的值域为　　　　　　 。

14．不等式(x－)≤0(x＞0)的解集是　　　　　 。