
6.双曲线C1: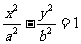
 的左准线为
的左准线为 ,左焦点和右焦点分别为F1和F2;抛物线C2的准线为
,左焦点和右焦点分别为F1和F2;抛物线C2的准线为 ,焦点为F2;C1与C2的一个交点为M,则
,焦点为F2;C1与C2的一个交点为M,则 等于 。
等于 。
5.在约束条件 下(如下图),当
下(如下图),当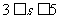 时,目标函数
时,目标函数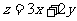 的最大值的变化范围是 。
的最大值的变化范围是 。

4.连掷两次骰子得到的点数分别为 和
和 ,记向量
,记向量 与向量
与向量 的夹角为
的夹角为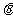 ,则
,则 的概率是 。
的概率是 。
3.已知 展开式中,各项系数的和与其各项二项式系数的和之比为64,则
展开式中,各项系数的和与其各项二项式系数的和之比为64,则 等于 。
等于 。
2.平面 外有两条直线
外有两条直线 和
和 ,如果
,如果 和
和 在平面
在平面 内的射影分别是
内的射影分别是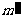 和
和 ,给出下列四个命题:
,给出下列四个命题:
① ; ②
; ② ;
;
③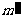 与
与 相交
相交
 与
与 相交或重合; ④
相交或重合; ④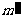 与
与 平行
平行
 与
与 平行或重合。
平行或重合。
其中不正确的命题个数是 个。
1.设 和
和 是两个集合,定义集合
是两个集合,定义集合 ,如果
,如果 ,
,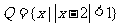 ,那么
,那么 等于 。
等于 。
20.(本小题满分14分)
已知 (m为常数,m>0且
(m为常数,m>0且 )
)
设 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.
(1)求证:数列{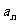 }是等比数列;
}是等比数列;
(2)若 ,且数列
,且数列 的前n项和
的前n项和 ,当
,当 时,求
时,求 ;
;
(3)若 ,问是否存在m,使得
,问是否存在m,使得 中每一项恒小于它后面的项?
中每一项恒小于它后面的项?
若存在,求出m的范围;若不存在,说明理由.
19.(本小题满分14分)
如下图,某小区准备绿化一块直径为 的半圆形空地,
的半圆形空地,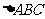 外的地方种草,
外的地方种草,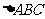 的内接正方形
的内接正方形 为一水池,其余地方种花.若
为一水池,其余地方种花.若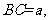
 ,设
,设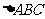 的面积为
的面积为 ,正方形
,正方形 的面积为
的面积为 ,将比值
,将比值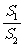 称为“规划合理度”.
称为“规划合理度”.

(1)试用 ,
, 表示
表示 和
和 .
.
(2)当 为定值,
为定值, 变化时,求“规划合理度”取得最小值时的角
变化时,求“规划合理度”取得最小值时的角 的大小.
的大小.
18.(本小题满分14分)
一辆邮政车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),每停靠一站便要卸下前面各站发往该站的邮袋各一个,同时又要装上该站发往后面各站的邮袋各一个,设该车从各站出发时邮政车内的邮袋数构成一个有穷数列 ,
, 试求:(1)
试求:(1)
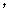
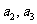
(2)邮政车从第k站出发时,车内共有邮袋数是多少个?
(3)求数列 的前 k项和
的前 k项和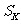 并证明:
并证明:
17.(本小题满分14分)
已知函数 图像上的点
图像上的点 处的切线方程为
处的切线方程为
 .
.
(1)若函数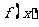 在
在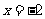 时有极值,求
时有极值,求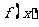 的表达式
的表达式
(2)函数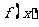 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com