3．函数的对称中心可以是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．x=π　　　　　　　　　 B．　　　　　　　 C．　　　　　　　 D．(π，0)

2．点P₁，P₂，P₃三点都在直线l上，且||=||，则点P分的比为　　　 (　　 )

　　　 A．1　　　　　　　　　　　　 B．1或-3　　　　　　　 C．2　　　　　　　　　　　　 D．-3

1．集合，则以下是A的真子集的是　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．[1，7]　　　　　　　　 B．[-1，5]　　　　　　 C．[-2，5]　　　　　　 D．[1，2]

22．某初级中学共有学生2000名，各年级男、女生人数如下表：

	初一年级	初二年级	初三年级
女生	373
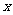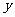男生	377	370

已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.

(1)求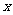的值；

(2)现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？

(3)已知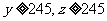，求初三年级中女生比男生多的概率。

21．下图是一个直三棱柱(以A₁B₁C₁为底面)被一平面所截得到的几何体，截面为ABC．已知A₁B₁＝B₁C₁＝l，∠A_lB_lC₁＝90°，AA_l＝4，BB_l＝2，CC_l＝3。

(1)设点O是AB的中点，证明：OC∥平面A₁B₁C₁；

(2)求直线BC与平面ACC₁A₁所成的角的大小；

(3)求此几何体的体积；

20．在数列{a_n}中，a₁=1, a_n+1=2a_n+2^n.

　 (1)设．证明：数列是等差数列；　　

　 (2)求数列的前项和．

19．已知圆心为C的圆经过点A(－1，1)和B(－2，－2)，且圆心在直线L：x+y－1=0上，求

　 (1)求圆心为C的圆的标准方程；

　 (2)设点P在圆C上，点Q在直线x－y+5=0上，求|PQ|的最小值。

　 (3)若直线kx－y+5=0被圆C所截得弦长为8，求k的取值。

18．已知甲盒内有大小相同的3个红球和2个黑球，乙盒内有大小相同的3个红球和3个黑球，现从甲、乙两个盒子内各任取2个球。

　 (1)求取出的4个球均为红球的概率；

　 (2)求取出的4个球中至少有1个红球的概率。

17．已知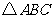的周长为，且．

　 (1)求边的长；

　 (2)若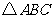的面积为，求角的度数．

16．若不等式｜3x-b｜＜4的解集中的整数有且仅有1，2，3，则b的取值范围为________.

第Ⅱ卷