
22.(本小题共14分)
已知函数 ,将满足
,将满足 的所有正数
的所有正数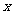 从小到大排成数列
从小到大排成数列 ,记
,记 .
.
(Ⅰ)证明数列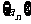 为等比数列;
为等比数列;
(Ⅱ)设 ,求
,求 ;
;
(Ⅲ)若 ,试比较
,试比较 与
与 的大小.
的大小.
21.(本小题共12分)
设定义在R上函数 的图象与函数
的图象与函数 (
( 为常数)的图象关于直线
为常数)的图象关于直线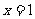 对称.
对称.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)设 ,当
,当 时,判断
时,判断 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
20.(本小题满分12分)
某超市计划销售一种水果,已知水果的进价为每盒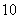 元,并且水果的进货量由销售量决定.预计这种水果以每盒
元,并且水果的进货量由销售量决定.预计这种水果以每盒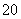 元的价格销售时该超市可销售
元的价格销售时该超市可销售 盒,经过市场调研发现每盒水果的价格在每盒
盒,经过市场调研发现每盒水果的价格在每盒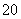 元的基础上每减少一元则增加销售
元的基础上每减少一元则增加销售 盒,而每增加一元则减少销售
盒,而每增加一元则减少销售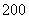 盒,现设每盒水果的销售价格为
盒,现设每盒水果的销售价格为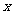
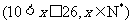 元.
元.
(Ⅰ)求销售这种水果所获得的利润 (元)与每盒水果的销售价格
(元)与每盒水果的销售价格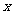 的函数关系式;
的函数关系式;
(Ⅱ)当每盒水果的销售价格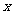 为多少元时,销售这种水果所获得的利润
为多少元时,销售这种水果所获得的利润 (元)最大,并求出最大值.
(元)最大,并求出最大值.
19.(本小题共12分)
已知函数 ,将
,将 的图象先向右平移
的图象先向右平移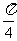 个单位,再向下平移2个单位后,所得到函数
个单位,再向下平移2个单位后,所得到函数 的图象关于直线
的图象关于直线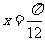 对称.
对称.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)已知 ,求
,求 的值.
的值.
18.(本小题共12分)
已知函数 的定义域为
的定义域为 ,解关于
,解关于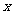 的不等式
的不等式 .
.
17.(本小题共12分)
在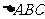 中,角
中,角 的对边分别为
的对边分别为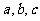 ,
,
(Ⅰ)证明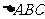 为等腰三角形;
为等腰三角形;
(Ⅱ)若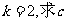 的值.
的值.
16.已知 是定义在
是定义在 上的偶函数,并且
上的偶函数,并且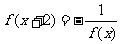 ,当
,当 时,
时, ,则
,则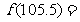 _________________.
_________________.
15.已知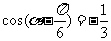 ,则
,则 的值为 .
的值为 .
14.若正实数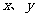 满足
满足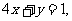 则
则 的最大值为
.
的最大值为
.
13.若等比数列 的前
的前 项和
项和 (
( 为常数),则
为常数),则 的值为 .
的值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com