18. (本小题满分12分)

　设定义在R上的函数f(x)＝a x⁴+b x³+c x在x＝－时取得极大值.且函数

y＝f′(x)的图象关于y轴对称.

(1)求函数f(x)的解析式；

　　 (2)求出函数f(x)在区间[－1，1 ]上的最大值和最小值；

(3)对任意x₁、x₂[－1，1 ]，求证：│f(x₁)－f(x₂)│≤.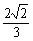

17. (本小题满分12分)

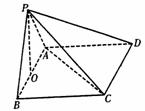
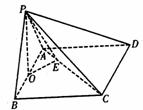
　　 如图，在四棱锥P－ABCD中，底面ABCD是正方形，△PAB是等边三角形，O是AB的中点，且POAC.

(1)求证：平面PAB平面ABCD；

(2)求二面角P－AC－B的正切值.

16. (本小题满分12分)

　　 已知α是锐角，且tan(α+)＝2. 求：

　　 (1)tanα的值.

　　 (2)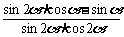的值.

15. 给出下列四个结论：

①“k＝1”“是函数y＝cos² k x－sin² k x的最小正周期为π”的充要条件.

②函数y＝sin(2 x－)沿向量a＝(，0)平移后所得图象的函数表达式是：

y＝cos2 x.

③函数y＝lg(a x²－2 a x+1)的定义域是R，则实数a的取值范围是(0，1).

④单位向量a、b的夹角是60°，则向量2a－b的模是.

其中不正确结论的序号是 　　　　.(填写你认为不正确的所有结论序号)

14. 一个人喝了少量酒后，血液中的酒精含量迅速上升到0.3mg/mL，在停止喝酒后，血液中的酒精含量以每小时25%的速度减少，为了保障交通安全，某地根据《道路交通安全法》规定：驾驶员血液中的酒精含量不得超过0.09 mg/mL，那么，一个喝了少量酒后的驾驶员，至少经过 　　　小时，才能开车？(精确到1小时).

13. 将锐角为∠BAD＝60°且边长是2的菱形ABCD，沿它的对角线BD折成60°的二面角，则：①异面直线AC与BD所成角的大小是 　　. ②点C到平面ABD的距离是 　　　.

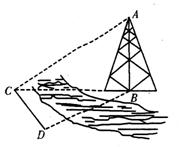
12. 如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个观测点C与D. 现测得∠BCD＝15°，∠BDC＝30°，CD＝30米，并在点C测得塔顶A的仰角为60°，则塔高AB＝ 　　　

11. 如图，函数f(x)的图像是折线段ABC，其中A，B，C的坐标分别为(0，4)，(2，0)，(6，4)，则f(f(0))＝　　 ；函数f(x)在x＝3处的导数f′(3)＝　　 .

10. 设f(x)是定义是R上恒不为零的函数，对任意x，y∈R，都有f(x)·f(y)＝f(x+y),若a₁＝，a_n ＝f(n)(n为正整数)，则数列{ a_n }的前n项和S_n的取值范围是(　 )

A. ≤S_n＜2　　　 B. ≤S_n≤2　　　　　 C. ≤S_n≤1　　　　 D. ≤S_n＜1

9. 设函数f(x)定义在实数集R上，它的图像关于直线x＝1对称，且当x≥1时，f(x)＝3^x－1，则有　　　　 　　　　　　　　　　　　　　　　　　　　　(　 )

A. f()＜f()＜f()　　　　　　　　 B. f()＜f()＜f()

　C. f()＜f()＜f()　　　　　　　　 D. f()＜f()＜f()