4、设全集U是实数集R，，则图中阴影部分所表示的集合是(　　 )

A．　　　 `　 B．C．　　　 D．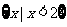

3、函数的递增区间是(　　　　　 )

A．[，2]　　　　　　　　　 B．(-∞，-1]　　　　　　　 C．[2，+∞)　　　　　　　　　　 D．[-1，]

2、若，则下列判断错误的是(　　　　 )

A．P或Q为真　　　　　　 B．P或Q为假　　　　 C．P且Q为假　　　　　　 D．P或Q为真

1、设集合的(　 　 )

A．充分不必要条件　　　　　　　　　 B．必要不充分条件　　

C．充要条件　　　　　　　　　　　　　　　 D．既不充分也不必要条件

21、(本小题满分14分)

已知函数f(x)=mx³+nx²(m、n∈R ,m≠0)的图像在(2，f(2))处的切线与x轴平行．

(1)求n，m的关系式并求f(x)的单调减区间；

(2)证明：对任意实数0<x₁<x₂<1, 关于x的方程：在(x₁,x₂)恒有实数解

(3)结合(2)的结论，其实我们有拉格朗日中值定理：若函数f(x)是在闭区间[a, b]上连续不断的函数，且在区间(a, b)内导数都存在，则在(a, b)内至少存在一点x₀，使得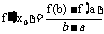．如我们所学过的指、对数函数，正、余弦函数等都符合拉格朗日中值定理条件．试用拉格朗日中值定理证明：

当0<a<b时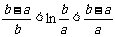，(可不用证明函数的连续性和可导性)

20．(本小题满分14分)

已知函数(为实数)，，．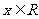

(1)若且函数的值域为，求的表达式；

(2)在(1)的条件下，当时，是单调函数，求实数k的取值范围；

(3)设，且为偶函数，判断+能否大于零．

19．(本题满分14分)

一场特大暴风雪严重损坏了某铁路干线供电设备，抗灾指挥部决定在24小时内完成抢险工程．经测算，工程需要15辆车同时作业24小时才能完成，现有21辆车可供指挥部调配．

(1)若同时投入使用，需要多长时间能够完成工程？(精确到0．1小时)

(2)现只有一辆车可以立即投入施工，其余20辆车需要从各处紧急抽调，每隔40分钟有一辆车可以到达并投入施工，问：24小时内能否完成抢险工程？说明理由．

18．(本小题满分14分)

已知函数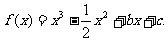

(1)若有极值，求b的取值范围；

(2)若在处取得极值时，当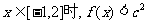恒成立，求c的取值范围；

(3)若在处取得极值时，证明：对[－1，2]内的任意两个值都有．

17．(本小题满分12分)

已知数列是等比数列,且

(1)求数列的通项公式;

(2)求证:

(3)设,求数列的前100项和．

16．(本小题满分12分)

已知A、B是△ABC内角，

(1)若A、B，求证：tanA•tanB>1；

(2)若B=，求sinA+sinC的取值范围．