20．(本题满分16分)已知两个二次函数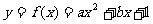：与

，函数图像与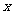轴有两个交点，其横坐标分别为()．

　 (1)证明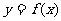：在(-1，1)上是单调函数；

　 (2)当时，设是方程的两实根，且，当时，试判断,的大小关系．

19．(本小题满分16分)在一个特定时段内，以点E为中心的7海里以内海域被设为警戒水域.点E 正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东且与点A相距40海里的位置B，经过40分钟又测得该船已行驶到点A北偏东+(其中sin=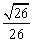，)且与点A相距10海里的位置C.

(1)求该船的行驶速度(单位：海里/小时)；

(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域，并说明理由.

18．(本小题满分15分)已知函数f(x)＝为偶函数，且函数y＝f(x)图象的两相邻对称轴间的距离为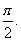

(1)求f()的值；

(2)将函数y＝f(x)的图象向右平移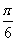个单位后，再将得到的图象上各点的横坐标舒畅长到原来的4倍，纵坐标不变，得到函数y＝g(x)的图象，求g(x)的单调递减区间.

17．(本小题满分15分)某商场在促销期间规定：商场内所有商品按标价的80%出售；同时当顾客在该商场内消费满一定金额后，按如下方案获得相应金额的奖券：

根据上述促销方法，顾客在该商场购物可以获得双重优惠．如购买标价为400元的商品，则消费金额为320元，获得的优惠为：400×0.2+30=110(元)．

设购商品得到的优惠率为　

试问：(1)若购买一件标价为1000元的商品，顾客得到优惠率是多少？

　　　　 (2)对于标价在[500，800](元)内的商品，顾客购买标价为多少元的商品，可　　　　　　　 得到不小于的优惠率？

16．(本小题满分14分)在△ABC中，角A、B、C的对边分别是a、b、c，且A为锐角，

　 (1)求f(A)的最小值；

　 (2)若，求b的大小．

15．(本题满分14分)集合,，若 “”是

　“”的充分条件，求 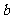的取值范围．

14．如图所示,△ABC中，BC边上的两点D 、E分别与A连线．假设，三角形ABC，ABD，ABE的外接圆直径分别为，则满足的不等关系是　 　 　　 　．

13．已知函数y=的最大值为M,最小值为m,则的值为　　　　　 ．

12．已知向量p =(2，x-1)，q=(x，-3)，且p⊥q，若由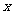的值构成的集合满足,则实数构成的集合是___________.

11．已知向量集合M={a | a =(1，2)+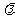(3，4)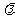，∈R}，N={b | b =(-2，-2)+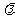(4，5)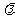，∈R}，则M∩N=_____　　 __．