
18.(本小题满分14分)
如下图,把边长为1的正方形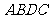 沿对角线
沿对角线 折起得到三棱锥
折起得到三棱锥 ,
, 是
是 边上一点.
边上一点.

(Ⅰ)求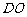 的取值范围;
的取值范围;
(Ⅱ)当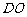 取最小值时,证明:
取最小值时,证明: 平面
平面 ;
;
(Ⅲ)若 ,求二面角
,求二面角 的余弦值.
的余弦值.
17.(本小题满分14分)
已知函数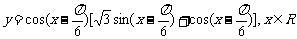 .
.
(Ⅰ)求函数 的最大值及相应的自变量
的最大值及相应的自变量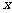 的集合;
的集合;
(Ⅱ)该函数的图象可由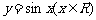 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
16.(本小题满分14分)
同时抛掷4枚均匀的硬币80次,设4枚硬币正好出现2枚正面向上,2枚反面向上的次数为ξ.
(Ⅰ) 求抛掷4枚硬币,恰好2枚正面向上,2枚反面向上的概率;
(Ⅱ) 求 的数学期望和方差.
的数学期望和方差.
(二)选做题:第13、14、15题是选做题,考生只能选做二题,三题全答的,只计算前两题的得分.
13.(坐标系与参数方程选做题)在极坐标系中,以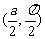 为圆心,
为圆心, 为半径的圆的极坐标方程是
,该圆与极轴平行的切线的极坐标方程是
.
为半径的圆的极坐标方程是
,该圆与极轴平行的切线的极坐标方程是
.
14.(不等式选讲选做题)已知 为正数,且
为正数,且 ,则
,则 的最大值是
,
的最大值是
, 取得最大值时
取得最大值时 .
.
15.(几何证明选讲选做题)如图,从圆 外一点
外一点 引圆的切线
引圆的切线 和割线
和割线 ,已知
,已知 ,圆
,圆 的半径为
的半径为 ,圆心
,圆心 到
到 的距离为
的距离为 ,则
,则 ,
, .
.

(一)必做题:第9、10、11、12题是必做题,每道试题考生都必须做答.
9.一个几何体的三视图如图所示,若它的正视图和侧视图都是矩形,俯视图是一个正三角形,则这个几何体的表面积是 ;体积是 .

10.若 的展开式中,第6项的二项式系数最大,则展开式中的常数项为 .
的展开式中,第6项的二项式系数最大,则展开式中的常数项为 .
11.利用定积分的几何意义,计算: .
.
12.设数列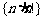 的前
的前 项和为
项和为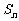 ,则
,则 = ,当
= ,当 时,
时,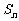 = .
= .
8.如下图所示的框图算法中,若输入 ,则输出的
,则输出的 ( )
( )

A.239 B.494 C.1004 D.2024
7.一个袋中装有大小相同的5只白球和3只红球,现在不放回的取2次,记“第1次拿出的是白球”为事件 ,“第2次拿出的是白球”为事件
,“第2次拿出的是白球”为事件 ,则事件
,则事件 与
与 同时发生的概率是( )
同时发生的概率是( )
A. B.
B. C.
C. D.
D.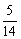
6.给出下列命题:①对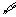 实数
实数 ,都
,都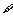 一个实数
一个实数 ,使得
,使得 ;②两个非零向量a与b垂直的充要条件是|a+b|=|a-b|;③如果两条直线
;②两个非零向量a与b垂直的充要条件是|a+b|=|a-b|;③如果两条直线 和平面
和平面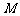 满足
满足 ,且
,且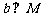 ,则
,则 ;④
;④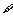 一个实数
一个实数 ,使
,使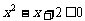 .其中真命题的序号是( )
.其中真命题的序号是( )
A.②③④ B.②③ C.②④ D.①③
5.已知双曲线的一条渐近线方程为 ,且点
,且点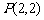 在此双曲线上,则双曲线的离心率为( )
在此双曲线上,则双曲线的离心率为( )
A. B.5 C.
B.5 C. D.3
D.3
4.已知 ,则
,则 的单调递增区间是( )
的单调递增区间是( )
A. B.
B. C.
C.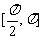 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com