
5、实数a、b、c不全为0的条件是( )
A.a、b、c均不为0; B.a、b、c中至少有一个为0;
C.a、b、c至多有一个为0; D.a、b、c至少有一个不为0。
4、演绎推理是以下列哪个为前提,推出某个特殊情况下的结论的推理方法( )
A.一般的原理原则; B.特定的命题; C.一般的命题; D.定理、公式。
3、下列表述正确的是( )
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理。
A.①②③; B.②③④; C.②④⑤; D.①③⑤。
2、类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四面体的下列哪些性质,你认为比较恰当的是( )
①各棱长相等,同一顶点上的任两条棱的夹角都相等;②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;③各个面都是全等的正三角形,同一顶点上的任两条棱的夹角都相等
A.①; B.①②; C.①②③; D.③。
1、由数列1,10,100,1000,……猜测该数列的第n项可能是( )
A.10n; B.10n-1; C.10n+1; D.11n.
22.(本小题满分14分)
(理)已知函数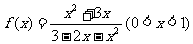 的反函数为
的反函数为 ,设它在点
,设它在点 处的切线在
处的切线在 轴上的截距为
轴上的截距为 ,数列{
,数列{ }满足:
}满足: ,
, 。
。
(1)求数列{ }的通项公式;
}的通项公式;
(2)在数列 中,仅当
中,仅当 时,
时,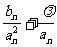 取最小值,求
取最小值,求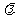 的取值范围;
的取值范围;
(3)令函数 ,数列{
,数列{ }满足:
}满足: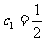 ,
,
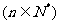 ,求证:对于一切
,求证:对于一切 的正整数,都满足:
的正整数,都满足: 。
。
(文)已知函数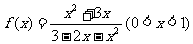 的反函数为
的反函数为 ,数列{
,数列{ }满足:
}满足: ,
, 。
。
(1)求数列{ }的通项公式;
}的通项公式;
(2)设函数 在点
在点 处的切线在
处的切线在 轴上的截距为
轴上的截距为 ,求数列{
,求数列{ }的通项公式;
}的通项公式;
(3)在数列 中,仅当
中,仅当 时,
时, 取最大值,求
取最大值,求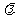 的取值范围;
的取值范围;
21.(本小越满分12分)
已知双曲线
 的离心率为
的离心率为 ,F1、F2分别为左、右焦点,M为左准线与渐近线在第二象限内的交点,且
,F1、F2分别为左、右焦点,M为左准线与渐近线在第二象限内的交点,且 。
。
(1)求双曲线的方程;
(2)设A( ,0),B(
,0),B(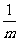 ,0)(
,0)(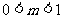 )是
)是 轴上的两点,过点A作斜率不为0的直线
轴上的两点,过点A作斜率不为0的直线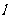 ,使得
,使得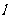 交双曲线于C、D两点,设直线BC交双曲线于另一点E。证明:直线DE垂直于
交双曲线于C、D两点,设直线BC交双曲线于另一点E。证明:直线DE垂直于 轴。
轴。
20.(本小题满分12分)
(理)已知A、B、C是直线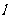 上的三点,向量
上的三点,向量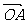 ,
, ,
, 满足:
满足: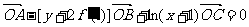 ,函数
,函数 。
。
(1)求函数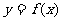 表达式;
表达式;
(2)若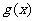 在点(3,
在点(3, )处的切线与直线
)处的切线与直线 平行,求函数
平行,求函数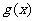 的极值;
的极值;
(3)若函数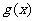 在(0,2)上单调递减,求实数
在(0,2)上单调递减,求实数 的取值范围。
的取值范围。
(文)已知A、B、C是直线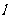 上的三点,且满足:
上的三点,且满足: 。
。
(1)若 在点(3,
在点(3, )处的切线与直线
)处的切线与直线 平行,求函数
平行,求函数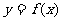 的极值;
的极值;
(2)若函数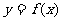 在(-2,-
在(-2,- )上单调递减,求实数
)上单调递减,求实数 的取值范围。
的取值范围。
19.(本小题满分12分)
如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面△PBC是等边三角形,且平面PBC⊥平面ABCD,∠ABC=45°,AB= ,BC=4,E、F分别为PB、PA的中点。
,BC=4,E、F分别为PB、PA的中点。

(1)求异面直线BC与PA所成的角;
(2)求二面角P-EC-D的大小;
(3)求点A到截面EFDC的距离。
18.(本小题满分12分)
袋中装着标有数字1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用 表示取出的3个小球上的最大数字。
表示取出的3个小球上的最大数字。
(1)求取出的3个小球上的数字互不相同的概率;
(2)(理)求随机变量 的概率分布和数学期望。
的概率分布和数学期望。
(文)求计分介于20分到40分之间的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com