5、工人月工资(元)依劳动生产率(千元)变化的回归直线方程为，下列判断正确的是(　 )　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

A．劳动生产率为1000元时，工资为50元

B．劳动生产率提高1000元时，工资提高150元

C．劳动生产率提高1000元时，工资提高90元

D．劳动生产率为1000元时，工资为90元

4、两个变量与的回归模型中，分别选择了4个不同模型，它们的相关指数如下 ，其中拟合效果最好的模型是(　　 )

A．模型1的相关指数为0.98　　 B． 模型2的相关指数为0.80

C．模型3的相关指数为0.50　　 D． 模型4的相关指数为0.25

3、一位母亲记录了儿子3-9岁的身高，由此建立的身高与年龄的回归模型为y=7.19x+73.93

用这个模型预测这个孩子10岁时的身高，则正确的叙述是(　 )　　　　　　　　　　　

A．身高一定是145.83cm　　　　　 B．身高在145.83cm以上

C．身高在145.83cm以下　　　　　 D．身高在145.83cm左右

2、设两个变量x和y之间具有线性相关关系，它们的相关系数是r，y关于x的回归直线的斜率是b，纵截距是a，那么必有(　 )　　　 　　　　　　　　　　　　　　　　　　

A．　 b与r的符号相同　　　　 B．　 a与r的符号相同

C．　 b与r的相反　　　　　　 D．　 a与r的符号相反

1、　 在画两个变量的散点图时，下面哪个叙述是正确的(　 )

A．预报变量在轴上，解释变量在轴上

B．解释变量在轴上，预报变量在轴上　　

C．可以选择两个变量中任意一个变量在轴上

D．可以选择两个变量中任意一个变量在轴上

12．已知10只狗的血球体积及红血球的测量值如下(x(血球体积，mm)，y(血红球数，百万)):

(1)画出上表的散点图； (2)求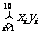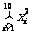，，，； (3)由散点图判断能否用线性回归方程来刻画与之间的关系，若能，求出线性回归方程.

11．在某年一项关于16艘轮船的研究中，船的吨位区间从192吨到3246吨，船员的数目从5人到32人.船员人数关于船的吨位的线性回归方程为

(1)假设两艘轮船吨位相差1000吨，则船员平均人数相差多少？

(2)对于最小的船估计的船员数是多少？对于最大的船估计的船员数是多少？(本小题保留整数)

10．变量与具有线性相关关系，当取值为16,14,12,8时，通过观测得到的值分别为11,9，8，5.若在实际问题中，的预报最大取值是10，则的最大取值不能超过多少？

9．下列说法中正确的是 　　　　　　　　　　(填序号)

①回归分析就是研究两个相关事件的独立性；②回归模型都是确定性的函数；③回归模型都是线性的；④回归分析的第一步是画散点图或求相关系数；⑤回归分析就是通过分析、判断，确定相关变量之间的内在的关系的一种统计方法.

8．下列结论中，能表示变量具有线性相关关系的是　　　 　

①　　　 ②　　　 ③　　　 ④