
2.长方体ABCD-A1B1C1D1中,若AB=BC=a,AA1=2a,则点D到平面A1BC的距离为( )
A. B.
B. C.
C. D.
D.
1.9名同学分成3组讨论问题,每组3人,共有不同的分组方法种数为 ( )
A. B.
B.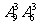 C.
C. D.
D.
22.(本小题14分)
已知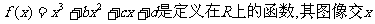 轴于A、B、C三点。点B的坐标为(2,0),且
轴于A、B、C三点。点B的坐标为(2,0),且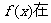 [-1,0]和[0,2]上有相反的单调性。
[-1,0]和[0,2]上有相反的单调性。
(Ⅰ)求c的值。
(Ⅱ)若函数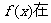 [0,2]和[4,5]上也有相反的单调性,
[0,2]和[4,5]上也有相反的单调性,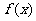 的图像上是否存在一点M,使得
的图像上是否存在一点M,使得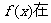 点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由。
点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由。
(Ⅲ)求|AC|的取值范围。
21.(本小题12分)
如图,斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面ABB1A1,AC=AB=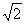 ,∠CAA1=∠BAA1=135°。
,∠CAA1=∠BAA1=135°。
(Ⅰ)求∠BAC的大小。
(Ⅱ)若底面△ABC重心为G,侧棱AA1=4,求GC1与平面A1B1C1所成角的大小。

20.(本小题12分)
令人瞩目的2008年奥运会即将在中国举行,为了迎接这次奥运盛会,成都市从某中学选出100名优秀学生代表,在举行奥运会之前每人至少参加一次社会公益活动,他们参加活动的次数统计如图所示。
(Ⅰ)求100名优秀学生代表参加活动的人均次数。
(Ⅱ)从100名优秀学生代表中任选两名,求他们参加活动次数恰好相等的概率。
(Ⅲ)从100名优秀学生代表中任选两名,求这两人参加活动次数之差的绝对值不小于1的概率。

19.(本小题12分)
已知函数
(Ⅰ)求实数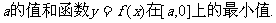
(Ⅱ)是否存在实数k,使得直线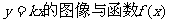 的图像恰有3个不同的交点?若存在,请求出k的取什范围;若不存在,请说明理由。
的图像恰有3个不同的交点?若存在,请求出k的取什范围;若不存在,请说明理由。
18.(本小题12分)
如图,在四棱锥P-ABCD中,底面ABCD为正方形,△PAB为等边三角形,O为AB的中点,且PO⊥AC。
(Ⅰ)求证:平面PAB⊥平面ABCD。
(Ⅱ)求D点到平面PBC距离
(Ⅲ)求二面角P-AC-B的大小。

17.(本小题12分)
甲、乙两人参加一项智力测试,已知在备选的10道题中,甲能答对其中的6道题,乙能答对其中的8道题,规定每位参赛者都从备选题中随机抽出3道题进行测试,至少答对2道题才算通过。
(Ⅰ)求甲恰好答对2道题的概率;
(Ⅱ)求甲、乙两人至少有一人通过测试的概率。
16.如图,函数 的图象在点P处的切线方程是
的图象在点P处的切线方程是
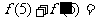 。
。

第Ⅱ卷
|
15.已知P、A、B、C是以O为球心的球面上的四个点,PA、PB、PC两两垂直,且PA=PB=PC=2,则球的表面积等于 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com