2．某校有教师300人，其中高级教师90人，中级教师150人，初级教师60人，为了了解教师的健康情况，从中抽取一个40人的样本，按分层抽样的方法抽取，其中高级教师的人数为____________.

1．计算的值是　　　　　　 ．

6.已知函数y=x³-3mx²-4n³(mn≠0),过原点作函数图象的一条切线,切点A恰好是函数的极值点.

　　　　 (1)讨论函数的单调性；

　　　　 (2)证明:m+n=0.

　　　　 (3)记f(x)=x³-3mx²-4n³(m<0),当x∈[-1,1]时,总有f(x)>-1,求m的取值范围.

5.修建一储粮仓库,形状如图5所示,底部为圆柱形,顶部为半球 形, 仓库侧面的每平方米造价是底面每平方米造价的4倍,顶部的每平方米造价是底面每平方米造价的5.5倍, 已知仓库底面的每平方米造价为15元,若修建仓库的总费用为9万元, 问仓库底面半径为多少米时,仓库的容积最大, 最大容积是多少(π取3计算)?

4.已知一枚质地不均匀的硬币,抛掷一次正面向上的概率为

　　　 (1)求抛掷这枚硬币三次, 恰有两次正面向上的概率；

　　　 (2)抛掷这枚硬币三次后, 再抛掷一枚质地均匀的硬币一次,求在这四次抛掷中恰有3次正面向上的概率.

3.如图4，四棱锥P－ABCD底面是边长为a的正方形，PD＝2a，PA＝PC＝a.

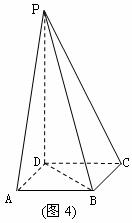
(1)求证:PD⊥平面ABCD；

(2)求CP与平面DPB所成角的大小.

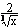　 1.已知(+　　 )ⁿ展开式的二项式系数之和为512,求该展开式中含有x²的项.

2.为迎接北京奥运会的召开,某校高二年级准备举行“奥运礼仪知识”竞赛,要求每班选派2名同学参赛,2名同学都获奖的班级为获胜班级.高二(1)派男生甲和女生乙参赛,若甲获奖的概率为0.55,乙获奖的概率为0.6,甲、乙是否获奖互不影响.求:

　　　 (1)两人中只有1人获奖的概率；

　　　 (2)该班为获胜班级的概率.

12.过点P(1,1)作曲线y=x³的切线,则切线的方程为　　　　　　 (　　 )

　　 A．3x-y-2=0　　　　　　　　　　　　　　 B．3x-4y+1=0或3x-y+2=0　　　　　　

C．3x-y-2=0或3x-4y+1=0　　　　　　　　 D．3x-y-2=0或3x-4y-1=0

11.某学校从6名教师志愿者中，选出4人到地震灾区支教，他们将分别去往汶川、青川、北川、都江堰, 若其中甲、乙两人不能派往都江堰, 则不同的选派方案共有(　　 )

A．96种　　 　　　B．180种　　　 　　　C．240种　　　 　　　　D．280种

10.已知函数f(x)=x³+3(k-1)x²-k²+1在(0,4)内单调递减, 则k的取值范围是　　　　 (　　 )

　　　 　A．(-∞,－1)　　　　　　　 B． (-∞,-1]　　　　　　　 C．(1, +∞)　　　　　　　　　　 D．[1, +∞)