
22.(本小题满分14分)已知数列{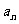 }中,
}中,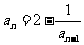 (n≥2,
(n≥2,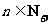 ),
),
(1)若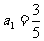 ,数列
,数列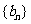 满足
满足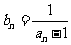 (
(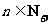 ),求证数列{
),求证数列{ }是等差数列;
}是等差数列;
(2)在(1)的情况下,求数列{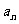 }中的最大项与最小项,并说明理由;
}中的最大项与最小项,并说明理由;
(3)若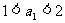 ,试证明:
,试证明: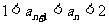 .
.
21.(本小题满分12分)  是以
是以 为焦点的双曲线C:
为焦点的双曲线C: (a>0,b>0)上的一点,已知
(a>0,b>0)上的一点,已知 =0,
=0, .(1)试求双曲线的离心率
.(1)试求双曲线的离心率 ;(2)过点P作直线分别与双曲线两渐近线相交于P1、P2两点,当
;(2)过点P作直线分别与双曲线两渐近线相交于P1、P2两点,当 =-
=- ,
, =
= ,求双曲线的方程.
,求双曲线的方程.
20.(本小题满分12分)
某高速公路指挥部接到通知,24小时后将有一场超历史记录的大暴雨,为确保万无一失,指挥部决定在24小时内筑一道临时堤坝,以防山洪淹没正在紧张施工的隧道工程。经测算,除现有施工人员外,还须调用翻斗车搬运 立方米的土方。已知每辆翻斗车每小时可搬运的土方量为
立方米的土方。已知每辆翻斗车每小时可搬运的土方量为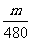 ,指挥部可调用25辆上述型号的翻斗车,但其中只有一辆可以立即投入施工,其余车辆需要从各处紧急抽调,每隔20分钟有一辆车到达并投入施工。
,指挥部可调用25辆上述型号的翻斗车,但其中只有一辆可以立即投入施工,其余车辆需要从各处紧急抽调,每隔20分钟有一辆车到达并投入施工。
(1)从第一辆车投入施工算起,第25辆车须多久才能到达?
(2)24小时内能否完成防洪堤坝工程?请说明理由。
19.(本小题满分12分)
如图,在直三棱柱ABC-A1B1C1中, AA1=4,AB=5
BC=3,AC=4,D为CC1的中点。
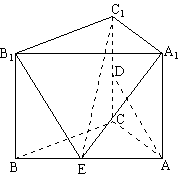
(1)求异面直线AD与A1B1所成角的余弦值;
(2)试在线段AB上找一点E,使得:A1E⊥AD;
(3)求点D到平面B1C1E的距离。
18.(本小题满分12分)已知函数f(x)=ax2+(b-8)x-a-ab , 当x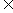 (-∞,-3)
(-∞,-3) (2,+∞)时, f(x)<0,当x
(2,+∞)时, f(x)<0,当x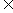 (-3,2)时f(x)>0 .
(-3,2)时f(x)>0 .
(1)求f(x)在[0,1]内的值域.
(2)若ax2+bx+c≤0的解集为R,求实数c的取值范围.
17. (本小题满分12分) 已知 ,且
,且
(1)求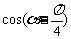 的值;
的值;
(2)求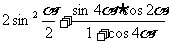 的值。
的值。
16.下列函数①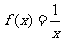 ;②
;②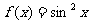 ;
;
③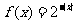 ;④
;④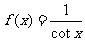 中,满足“存在与x无关的正常数M,使得
中,满足“存在与x无关的正常数M,使得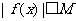 对定义域内的一切实数x都成立”的有 (把满足条件的函数序号都填上).
对定义域内的一切实数x都成立”的有 (把满足条件的函数序号都填上).
15.设实数 满足约束条件:
满足约束条件: ,则
,则 的最大值为
.
的最大值为
.
14.若数列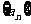 满足
满足 是首项为1,公比为2的等比数列,则
是首项为1,公比为2的等比数列,则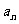 等于
。
等于
。
13.函数 的定义域是
。
的定义域是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com