
20.(本小题满分12分)
已知等差数列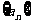 的前
的前 项和为
项和为 ,且
,且 ,等比数列
,等比数列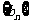 满足
满足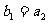 ,
,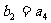 .
.
(1)求证: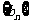 中的每一项均为
中的每一项均为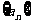 中的项;
中的项;
(2)若 ,数列
,数列 满足:
满足: ,求数列
,求数列 的前
的前 项和
项和 .
.
19.(本小题满分12分)
在进行一项掷骰子放球游戏中,规定:若掷出1点,甲盒中放一球;若掷出2点或3点,乙盒中放一球;若掷出4点,5点或6点,丙盒中放一球,前后共掷3次.设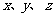 分别表示甲、乙、丙3个盒中的球数.
分别表示甲、乙、丙3个盒中的球数.
(1)求 依次成公差大于0的等差数列的概率.
依次成公差大于0的等差数列的概率.
(2)记 ,求随机变量
,求随机变量 的概率分布和数学期望.
的概率分布和数学期望.
18.(本小题满分12分)
如图,已知四棱锥S-ABCD中,SA 平面ABCD,在直角梯形ABCD中,AD∥BC,
平面ABCD,在直角梯形ABCD中,AD∥BC,
 ,SA=AD=
,SA=AD=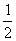 AB=1,M为BC的中点。
AB=1,M为BC的中点。
(1)求证:SM AD;
AD;
(2)求点D到平面SBC的距离;
(3)求二面角A-SB-C的大小。

17.(本小题满分12分)
已知函数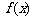 =
=
 .
.
(1)若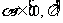 ,且sin2
,且sin2 =
= ,求f(
,求f( )的值;
)的值;
(2)若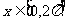 ,求函数
,求函数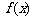 的单调递增区间.
的单调递增区间.
16.定义:若平面点集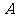 中的任一个点
中的任一个点 ,总存在正实数
,总存在正实数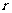 ,使得集合
,使得集合
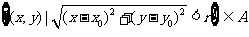 ,则称
,则称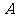 为一个开集.给出下列集合:
为一个开集.给出下列集合:
①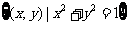 ;
②
;
② 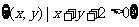 ;
;
③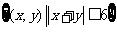 ; ④
; ④  .
.
其中是开集的是 .(请写出所有符合条件的序号)
15.在边长为1的正三角形ABC中,设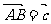 ,
, ,
,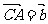 ,则
,则
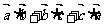 = .
= .
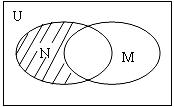
14.设全集 ,M=
,M= ,N=
,N=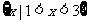 ,则图中阴影部分所表示的集合是
.
,则图中阴影部分所表示的集合是
.
13.圆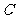 :x2 + y2
+ 6x + 5 = 0被直线
:x2 + y2
+ 6x + 5 = 0被直线 :
: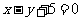 所截得的弦长为 .
所截得的弦长为 .
12.定义区间 ,
, ,
, ,
,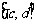 的长度均为
的长度均为 ,其中
,其中 .已知实数
.已知实数 ,则满足
,则满足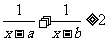 的
的 构成的区间的长度之和为
构成的区间的长度之和为
A. B.
B. C.
C. D.
D.
第Ⅱ卷(非选择题 共90分)
|
11.2008年春,我国南方部分地区遭受了罕见的特大雪灾.大雪无情人有情,厦门某中学组织学生在社区开展募捐活动,第一天只有10人捐款,人均捐款10元,之后通过积极宣传,从第二天起,每天的捐款人数是前一天的2倍,且人均捐款数比前一天多5元.则截止第5天(包括第5天)捐款总数将达到
A.4800元 B.8000元 C.9600元 D.11200元
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com